MATH 2B Lecture Notes - Lecture 4: Error Function, Farad, Antiderivative
MATH 2B verified notes
4/30View all
Document Summary
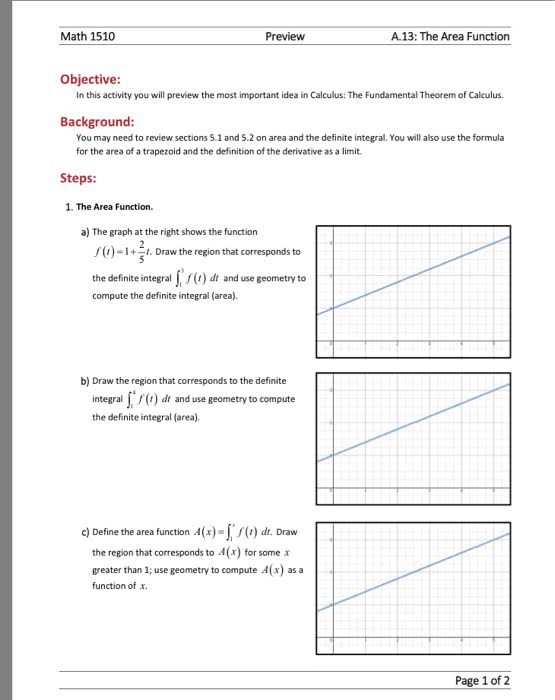
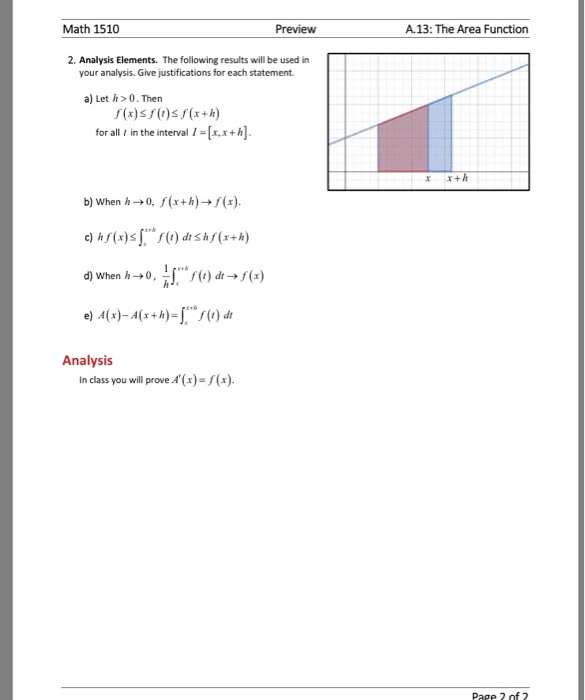
Math 2b - lecture 4 - the fundamental theorem of calculus. It is termed fundamental because it provides the link between the two branches of calculus: differentiation and integration. (definite) integration: find area under curve y=f(x) We need to first think of integrals as functions. We fix the lower limit of a definite integral to be a constant a and let the upper limit be variable. Thus if f is a function defined on an interval containing a and x, then (t)dt (x) g f is a function x a of x. The function g returns the net area under the curve y=f(x) from a up to x. Recall the conventions from the previous section for how to understand values and net area: in particular, net area is negative if either. Suppose that f is continuous on [a,b]. F differentiable on (a,b), and its derivative is. F (x) (x) (t)dt is continuous on [a,b], f x a.