MATH 2B Chapter Notes - Chapter 5.3: Differential Calculus, Continuous Function, Mean Value Theorem

• School: UC-Irvine
• Department: Mathematics
• Course: MATH 2B
• Professor: George Donaldson

Document Summary

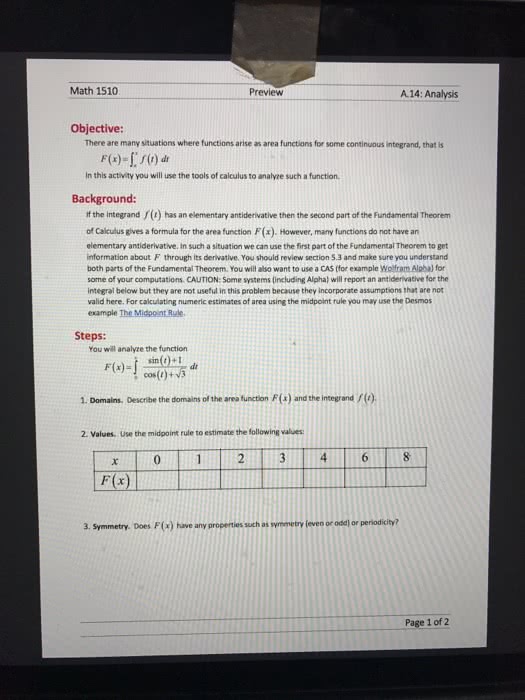
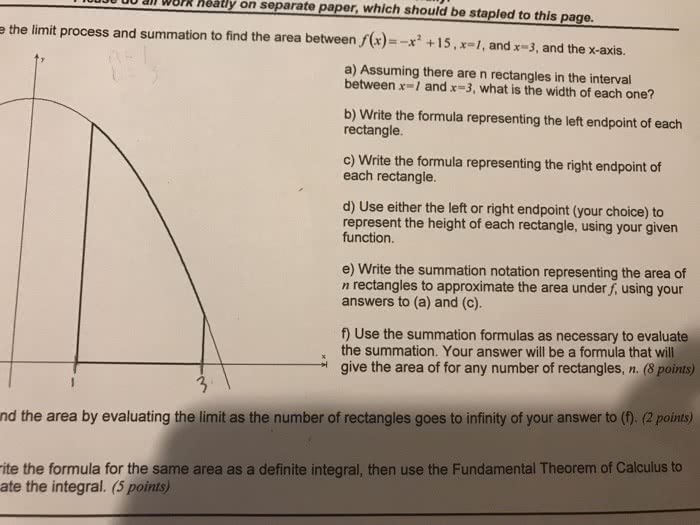
Anti-differentiation find f(x) such that f (x) = f (x) (de nite) integration find area under curve y = f (x) It is termed fundamental because it provides the link between the two branches of calculus: differen- tiation and integration. We rst need to think of integrals as functions. We x the lower limit of a de nite integral to be a constant a and let the upper limit be variable. Thus if f is a function de ned on an interval containing a and x, then g(x) = z x a f (t) dt is a function of x. The function g returns the net area under the curve y = f (x) from a up to x. Recall the conventions from the previous section for how to understand values and net area: particular, net area is negative if either in: x < a, or, f (t) < 0.