MATA02H3 Lecture Notes - Lecture 12: Modular Arithmetic, Euclidean Algorithm, Multiplication Table
MATA02H3 verified notes
12/18View all
Document Summary
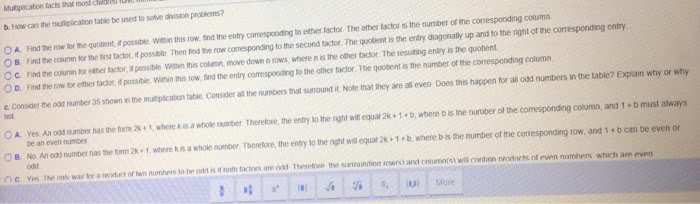
Mata02 - lecture 12 - solving modular arithmetic problems, euclidean algorithm, One pattern is that there are no numbers (let"s call this. B") such that 2 b=1 in mod 6 (if you see the 4th row, all you see are the numbers 0,4,2). Furthermore, there are no numbers such that 2 b=3 in mod 6. This indicates that 6 is composite and is the reason why not all numbers from 0-4 appear in every row and column. Let"s say that we take the module of a prime number, like 5. Here"s the multiplication table for it. gcd(3,6) = 3. Since 5 is a prime number, the gcd of it is 1 (this explains why every number from 0-4 are present in any row or column). 2x = 0 mod 6 gcd(4,5) = 1 gcd(3,5) = 1. 0 = 0 (since 6 is a multiple of 3, then mod of 6 would be 0)