MTH 162 Final: MTH 162 University of Rochester Fall 16Finalsol

25 views9 pages

turquoisegnu128

31 Jan 2019

School

University of Rochester

Department

Mathematics

Course

MTH 162

Professor

All

For unlimited access to Study Guides, a Grade+ subscription is required.

Document Summary

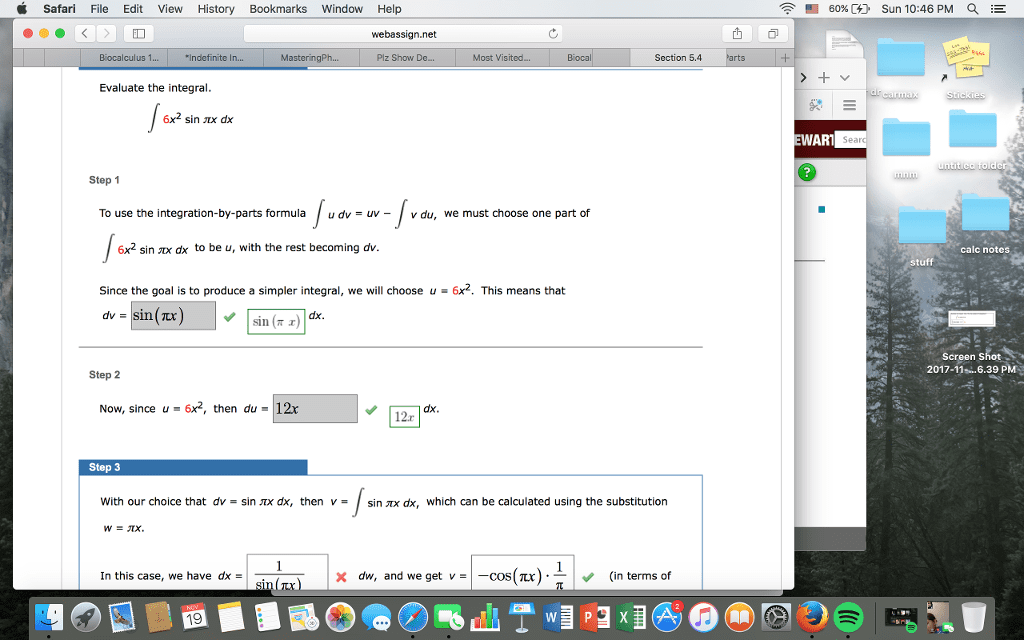
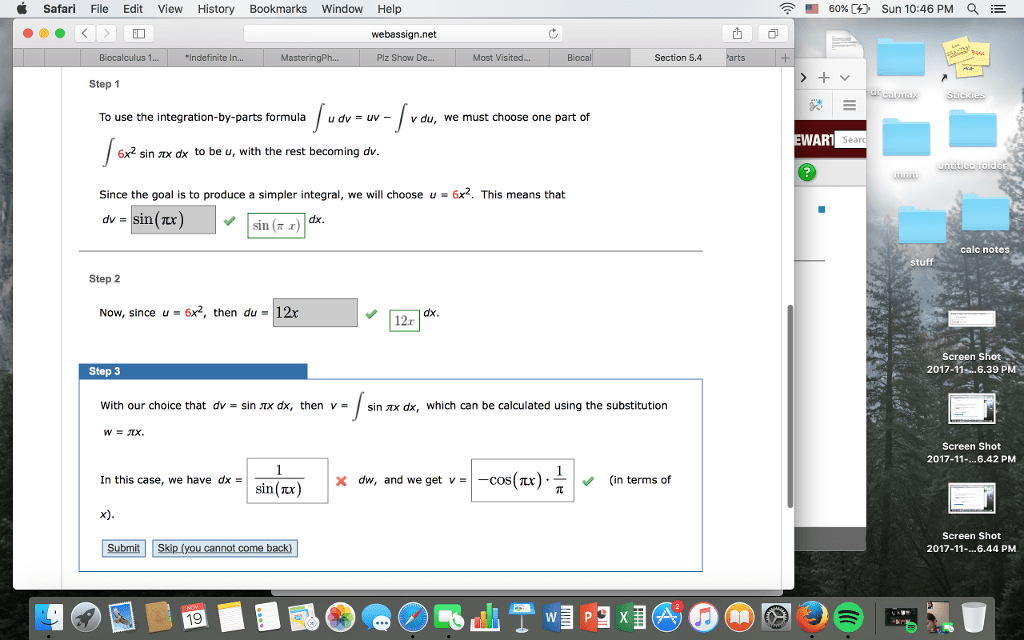
Part a: (15 points) evaluate the integral. 4 x2 dx = z 8 cos3 . 3 (cid:19) + c ( 4 x2)3 sin3 . Using the shell method we have shells of radius x, thickness dx and height (x3 + 1) 1 = x3. 5 (cid:12)(cid:12)(cid:12)(cid:12) (b) set up the integral for the volume of the region bounded by y = x4, y = 0 and x = 2 and rotated around line x = 2. Using the shell method we have shells of radius (2 x), thickness dx and height x4. Integrating by parts with u = arcsin x and dv = dx, we get du = dx. 1 x2 and v = x, so that the integral becomes. Z arcsin x dx = x arcsin x z x dx. Now make the substitution w = 1 x2, so dw = 2x dx and x dx = dw/2. Math 162 (calculus iia) and the original integral is.

Related Questions

Please show detailed steps/work thank u! really appriciate it !

1. (45 marks) Short-Answer Questions. Put your answer in the box provided but show your work also. Each question is worth 3 marks, but not all questions are of equal difficulty. Full marks will be given for correct answers placed in the box, but at most 1 mark will be given for incorrect answer. Unless otherwise stated, it is not necessary to simplify your answers in this question. a) Find the equation of the tangent plane to the graph of the function z = f(x,y) = sell at (0,1). Answer b) Evaluate (T, 0) if f(x,y) = sin(ry). Answer c) Graph of a function z = f(x,y) is given by: Which of the following level curves correspondes to this function. Answer d) If f(x,y) = e(3x – 2y), find lim - Math)-f(x,y) e) Find % if f(x, y) = x2 - y3 and 2 = r sin(t), y = r cos(t). Answer f) Evaluate the directional derivative of f(x, y) = !at (1, -1) in the direction of u =(2, 1). Answer 8) Does Simono converge? h) Sketch the direction field of the differential equation = 1-2y. i) Consider the differential equation ay = 15 - 31, y(0) = 0, and use Euler's method with step size 0.1 to estimate y(0.1). Answer j) Knowing that (-3,-3) is a critical point of f(x,y) = 2:3 + y2 – 4.cy -3.0, use the second derivative test to find out whether it is a local minimum, local maximum, or a saddle point. Answer k) Solve the initial value problem, dy dt 642 2y + cos(u) y(1) = . Answer 1) Is ū=(2,2, -1) perpendicular to v = (5,-4, 2)? Answer m) Find the area between the graph of y = 1 + sin(x) and y=1-sin(x) from 0 to 7. Answer n) Determine the lentgh of the curve y = 8/2,0 SIS 3. Evaluate and simplify your answer. Answer o) Express the volume of the solid obtained by rotating the bounded region that lies between curves y = (x-2)2 and y=1,150 $4 about the vertical line 2 = 5. Do not evaluate this integral. Answer

MTH 162 Final: MTH 162 University of Rochester Fall 16Finalsol

Document Summary

Get access

Related Documents

MTH 162 Final: MTH 162 University of Rochester Fall 15Finalsol

MTH 162 Midterm: MTH 162 University of Rochester Fall 15Exam1 Solutions2

MTH 162 Midterm: MTH 162 University of Rochester 162 Midterm 2 Fall 06

Related Questions