MATH 141 Lecture Notes - Lecture 10: Farad, Inverse Function

• School: University of Maryland
• Department: Mathematics
• Course: MATH 141
• Professor: Ruiwen Shu

Document Summary

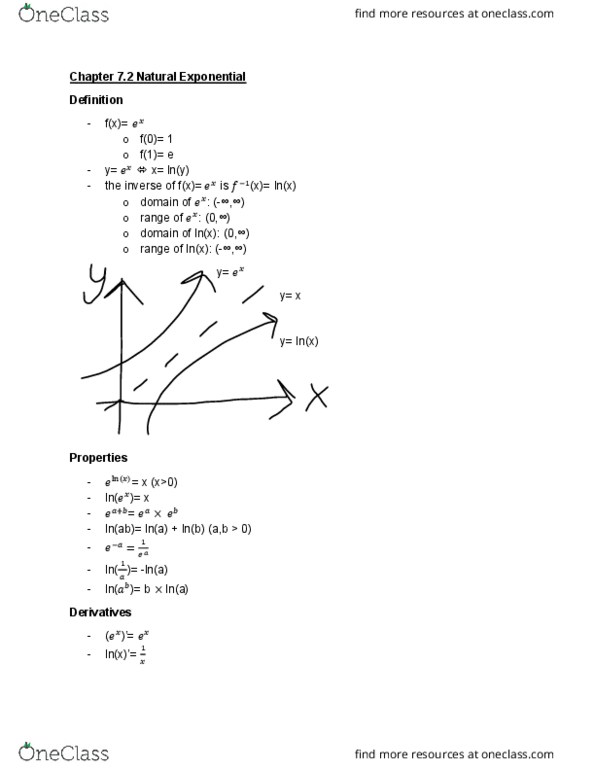
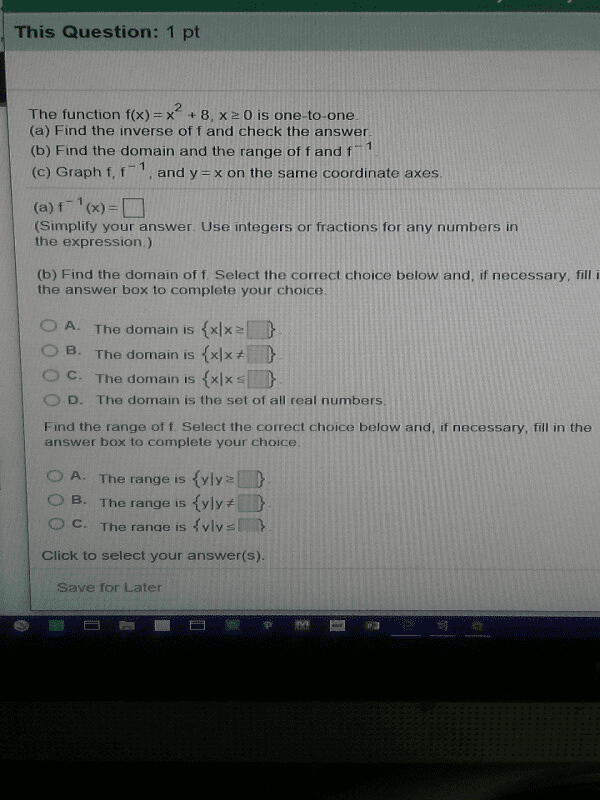
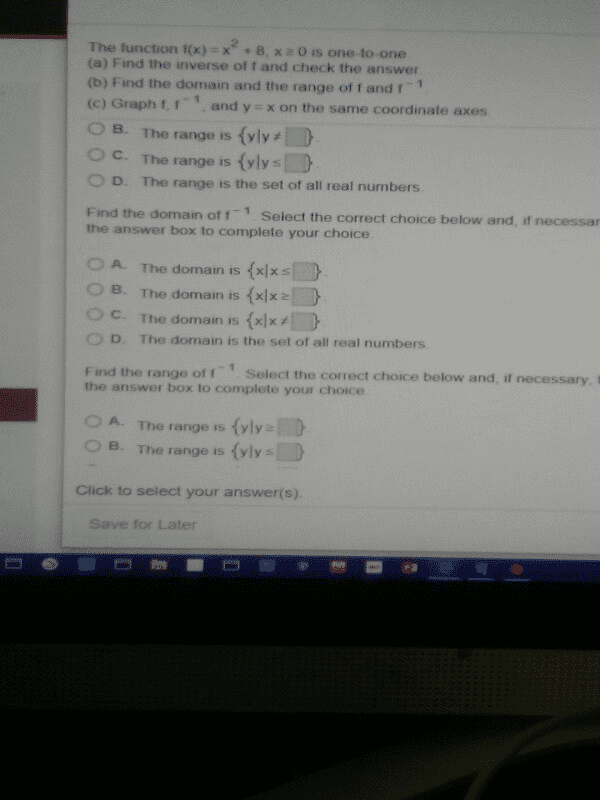
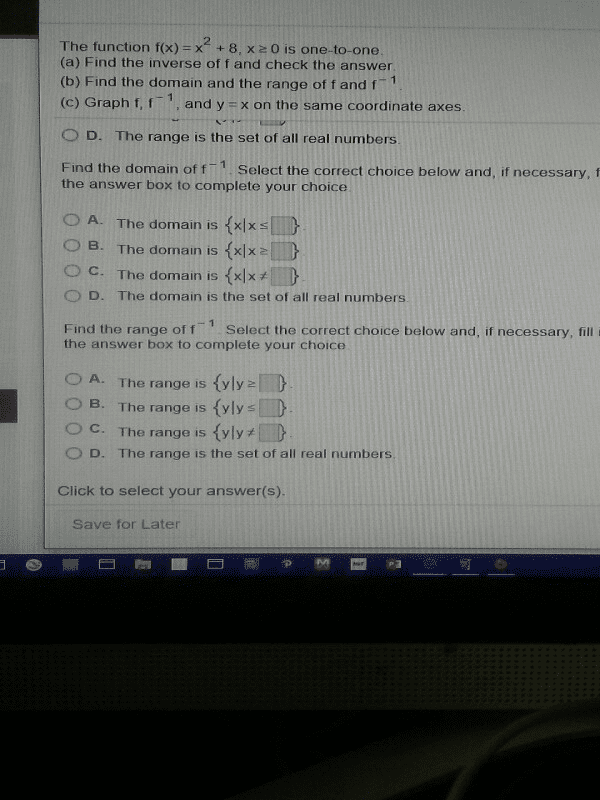
Definition f is a function: domain of f: [a,b, range of f: [c,d] G is the inverse function of f(denoted by (cid:2869)) if f(x)=y g(y)=x. Thus, the domain of (cid:2869)= range of f and range of (cid:2869)= domain of f : domain of (cid:2869)(y): [c,d, range of (cid:2869)(y): [a,b] For any y in the range of f, there is only one x with y=f(x) y= f(x) has an inverse, passes the horizontal line test y= f(x) does not have an inverse, 2 x"s with 1 y. Example: determine whether f has an inverse. If yes, find it: solve for x to find the inverse, then switch x and y at the end, no inverse, because parabolas have two x"s with one y. Find the inverse of f (when exist) Y= f(x) x= (cid:2869)(y: f(x)= (cid:1876)(cid:2870) (cid:884)(cid:1876), on (- , , f(x) on (- ,0, yes, (cid:2869)(x)= 1- (cid:883)+(cid:1876) y= (cid:1876)(cid:2870) (cid:884)(cid:1876) (cid:1876)(cid:2870) (cid:884)(cid:1876) (cid:1877)=(cid:882)