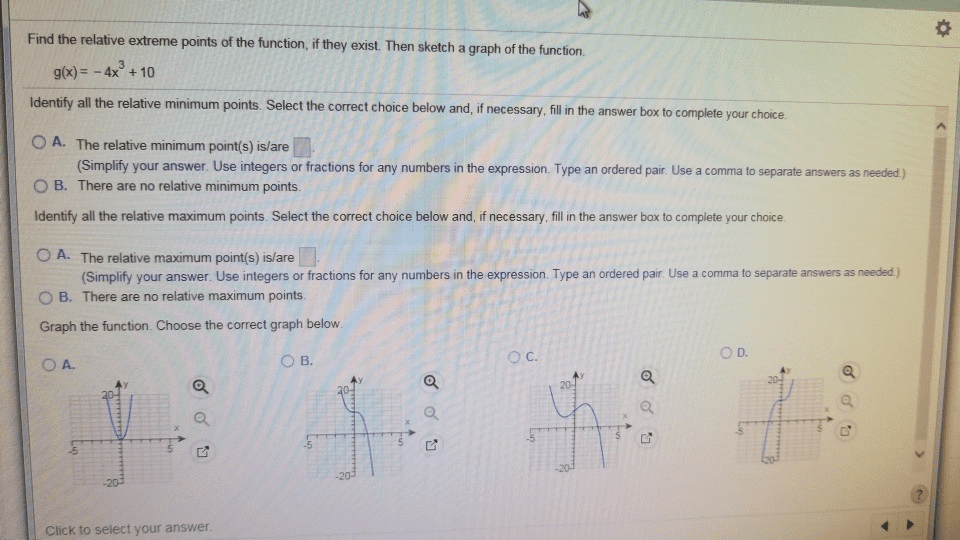
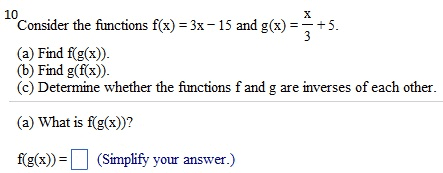Find the relative extreme points of the function, if they exist. Then sketch a graph of the function. g)x3+10 Identify all the relative minimum points. Select the correct choice below and, if necessary,fillin the answer box to complete your choice O A. The relative minimum point(s) is/are O B. There are no relative minimum points. Identify all the relative maximum points. Select the correct choice below and, if necessary, fill in the answer box to complete your choice (Simplify your answer. Use integers or fractions for any numbers in the expression. Type an ordered pair. Use a comma to separate answers as needed,) A. The relative maximum point(s) is/are 0 B. There are no relative maximum points. Graph the function. Choose the correct graph below. OA. (Simplify your answer. Use integers or fractions for any numbers in the expression. Type an ordered pair. Use a comma to separate answers as needed) O c. O D. G' Click to select your answer
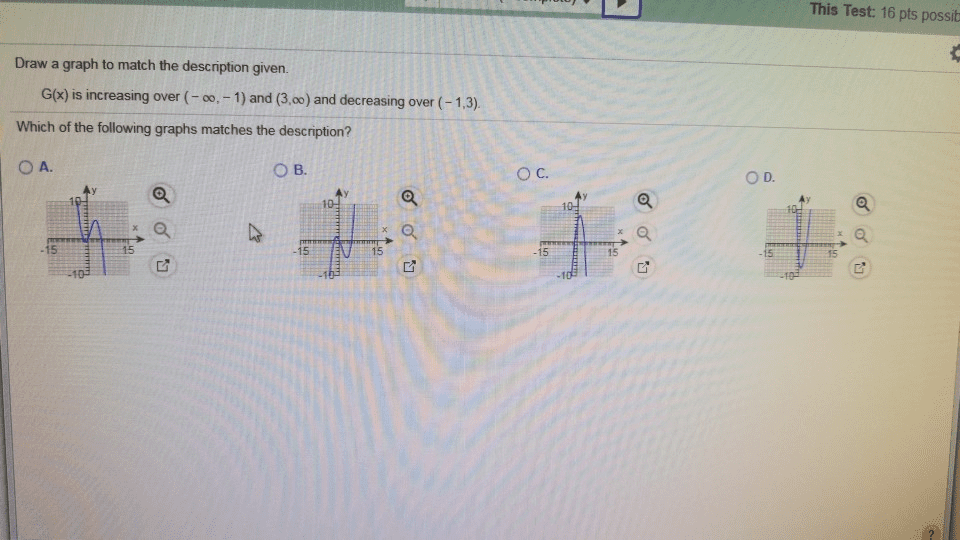
This Test: 16 pts possit Draw a graph to match the description given -1.3) G(x) is increasing over (-0,-1) and (3,oo) and decreasing over Which of the following graphs matches the description? O C. O A. 15 15 15 15 15 15 15 15 -1
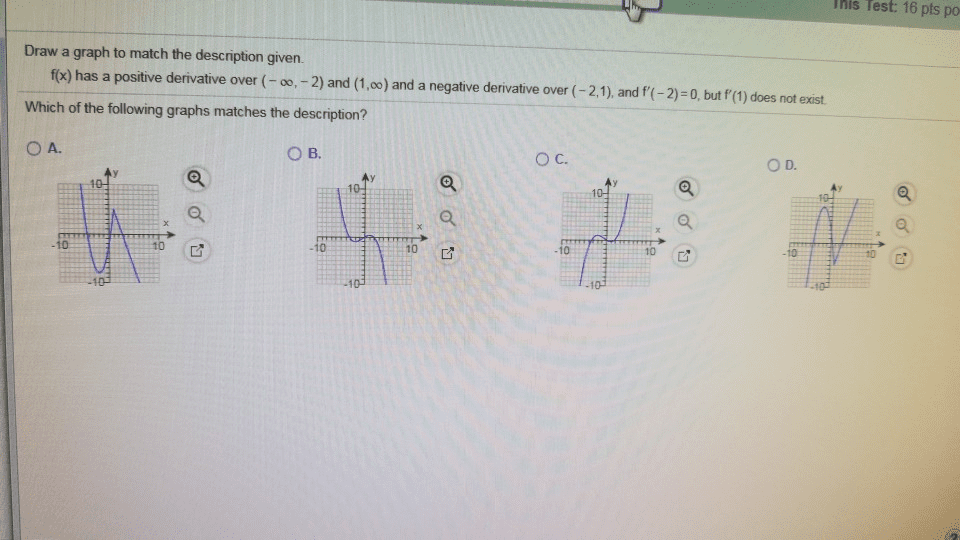
his Test: 16 pts po Draw a graph to match the description given. f(x) has a positive derivative over (-0,-2) and (1,00) and a negative derivative over (2,1), and f(-2)0, but f'(1) does not exist Which of the following graphs matches the description? O A. OB. O C. O D. 10 10 10 10ã 10 10ã
This Test: 16 pts possible Find all relative extrema and classity each as a maximum or minimum. Use the second-derivative test where possible. f(x)-64x 12x + 8 Identify all the relative minima. Select the correct choice below and, if necessary, ill in the answer box to complete your choice. O A. The relative minima are (Simplify your answer. Type an ordered pair. Use integers or fractions for any numbers in the expression. Use a comma to separate answers as needed) B. There is no relative minimum. Identify all the relative maxima. Select the correct choice below and. if necessary, fill in the answer box to complete your choice. A. The relative maxima are 1. (Simplify your answer. Type an ordered pair Use integers or fractions for any numbers in the expression. Use a comma to separate answers as needed ) O B. There is no relative maximum. Click to select and enter your answer(s)
This Test: 16 pts possible Sketch the graph of the following function. List the coordinates of where extrema or point well as where it is concave up or concave down. of inflection occur. State where the function is increasing or decreasing as t(x)=-x3 +9x2-54 What are the coordinates of the relative extrema? Select the correct choice below and, if necessary filli the answer box to complete your choice O A. The coordinates of the relative extrema are (Simplify your answer. Type an ordered pair. Type an exact answer using radicals as needed Use integers or fractions for any numbers in the expression Use a comma to separate answers as needed) B. There are no relative extrema. What are the coordinates of the inflection points? Select the correct choice below and, if necessary. fill in the answer box to complete your choice O A. The coordinates of the inflection points are (Simplify your answer. Type an ordered pair. Type an exact answer using radicals as needed Use integers or fractions for any numbers in the expression Use a comma to separate answers as needed.) OB. There are no inflection points On what interval(s) is f increasing or decreasing? O A. f is increasing on (-,0) and (6.o0) f is decreasing on (06) O B. f is increasing on (-0o,o), f is never decreasing O c. fis never increasing f is decreasing on (-oo,00) O D. fis increasing on (3.oo), f is decreasing on (-e 3) O E. f is increasing on (-,3) f is decreasing on (3.) Click to select your answer
Sketch the graph of the following function. List the coordinates of where extrema or points of inflection occur. State where the function is increasing or decreasing as well as where it is concave up or concave down fox)-x-4x3 +6 What are the coordinates of the relative extrema? Select the correct choice below and, if necessary, fill in the answer box to complete your choice OA. The coordinates of the relative extrema are (Simplify your answer. Type an ordered pair. Type an exact answer using radicals as needed Use integers or fractions for any numbers in the expression Use a comma to separate answers as needed) 0 B. There are no relative extrema. What are the coordinates of the inflection points? Select the correct choice below and, if necessary, filli the answer box to complete your choice â A. The coordinates of the inflection points are fy your answer Type an ordered pair. Type an exact answer using radicals as needed Use integers or fractions for a comma to separate answers as needed) (Simpli O B. There are no inflection points On what interval(s) is f increasing or decreasing? A. f is increasing on (-oc,0) and (2,00) f is decreasing on (02) â B. f is never increasing fis decreasing on (-oo, o) C. f is increasing on (-0,3), fis decreasing on (3,00) O D. fis increasing on (-00,0o) fis never decreasing O E. fis increasing on (0.2) fis decreasing on (+000 and (2,0) Click to select your answer
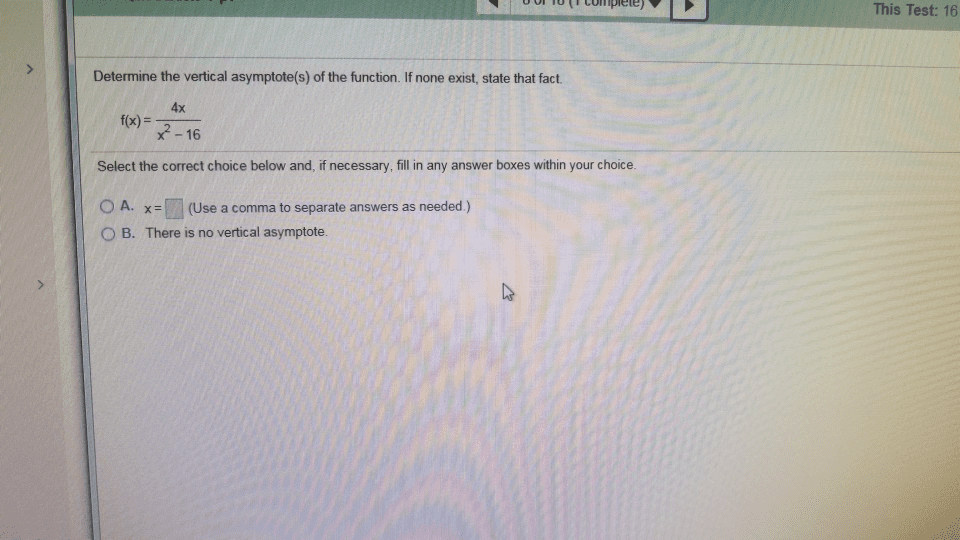
This Test: 16 Determine the vertical asymptote(s) of the function. If none exist, state that fact. 4x x2-16 Select the correct choice below and, if necessary, fill in any answer boxes within your choice O A. x-(Use a comma to separate answers as needed) O B. There is no vertical asymptote
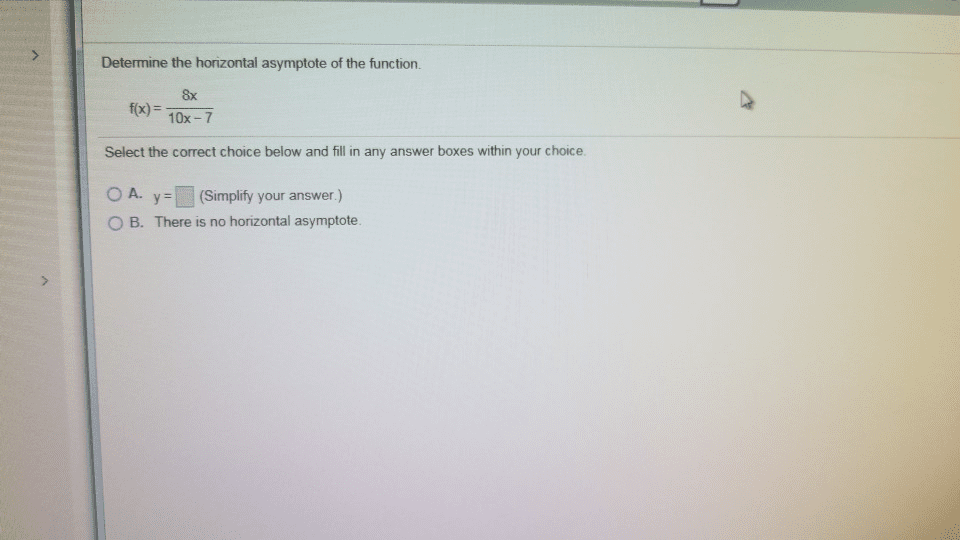
Determine the horizontal asymptote of the function. 8x fx)-10x-7 Select the correct choice below and fill in any answer boxes within your choice OA. y-11 (Simplify your answer.) O B. There is no horizontal asymptote.
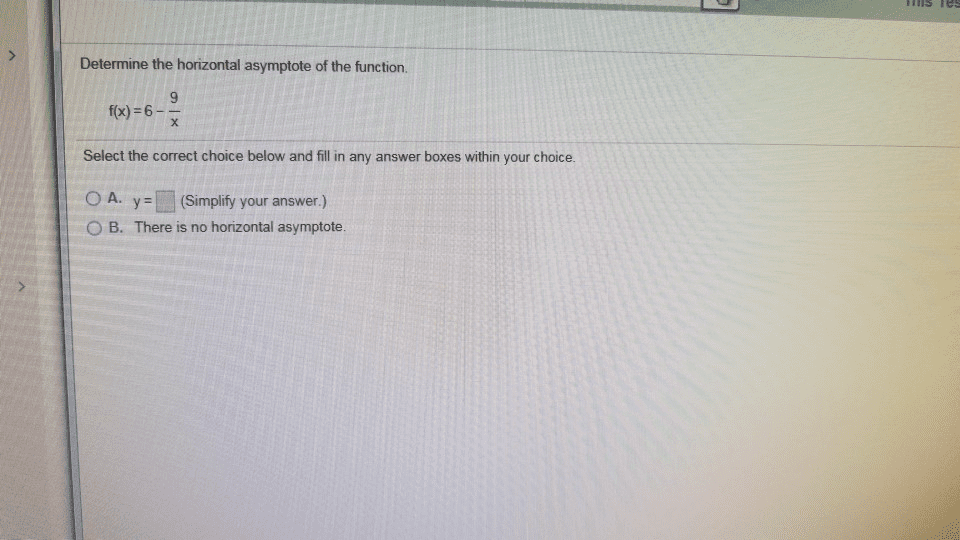
Determine the horizontal asymptote of the function. f(x)-6 Select the correct choice below and fill in any answer boxes within your choice. A. y -(Simplify your answer.) O B. There is no horizontal asymptote
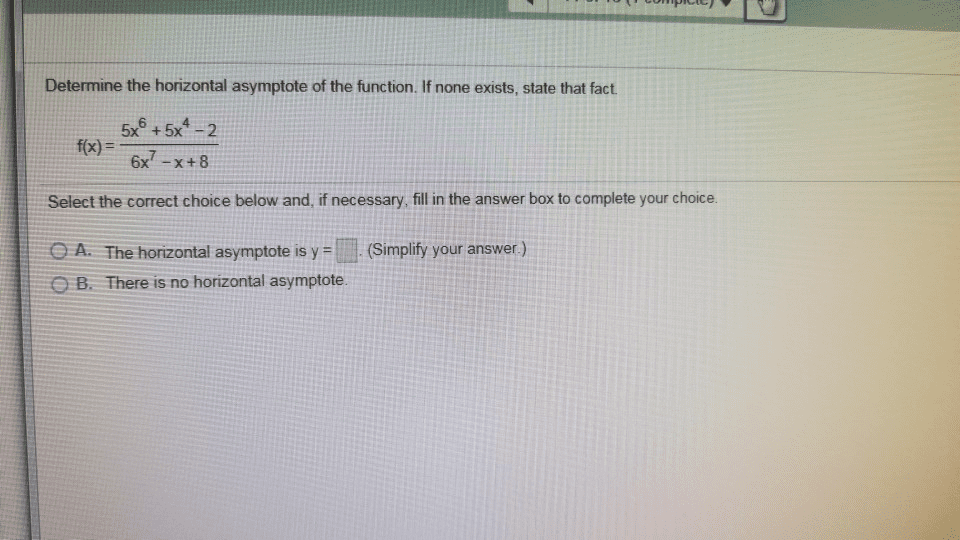
Determine the horizontal asymptote of the function. If none exists, state that fact 5x6 +5x42 fxi6x7 6x-x+8 Select the correct choice below and, if necessary, fill in the answer box to complete your choice OA The horizontal asymptote is y=ç.(Simplify your answer.) B. There is no horizontal asymptote
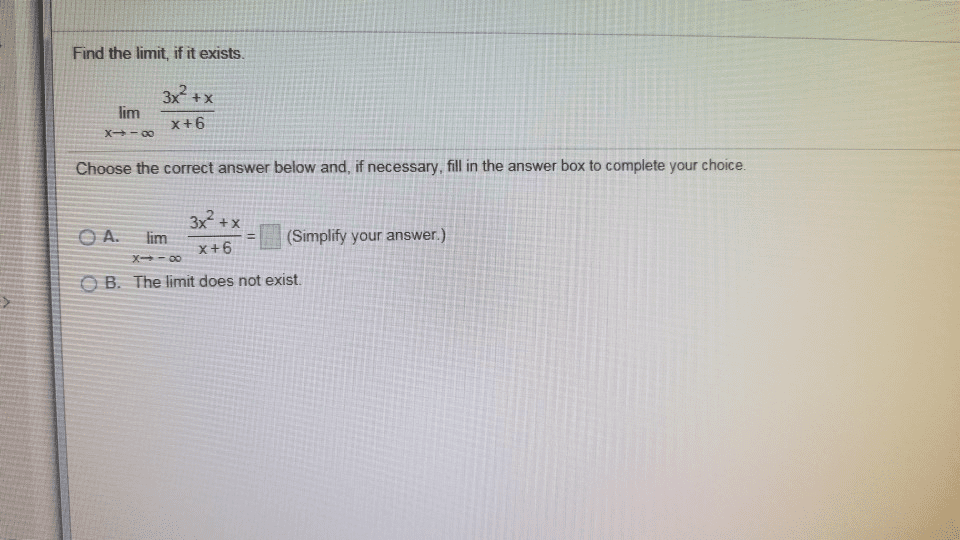
Find the limit, if it exists 32 +x lim x+6 Choose the correct answer below and, if necessary, fill in the answer box to complete your choice. OA. lim 3x+5=17 (Simplify your answer.) O B. The limit does not exist. X+6
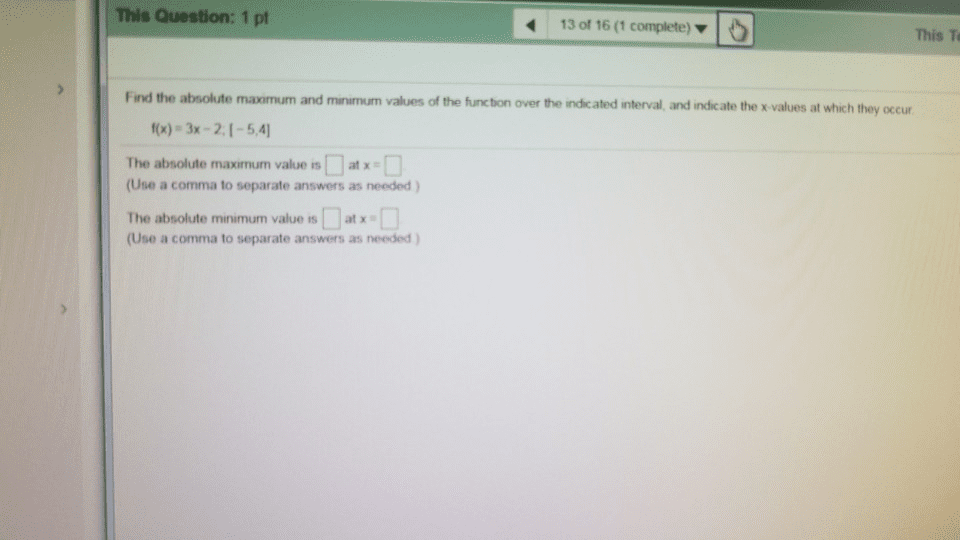
This Question: 1 pt 13of16 (1 complete) ⼠This T Find the absoute maximum and minimum values of the function over the indicated interval, and indicate the x values at which they occur tx)-3x-2.1-5,4 The absolute maximum value isat x (Use a comma to separate answers as needed) The absolute rm.nemurn value is [] at x-๠(Use a comma to separate answers as needed )
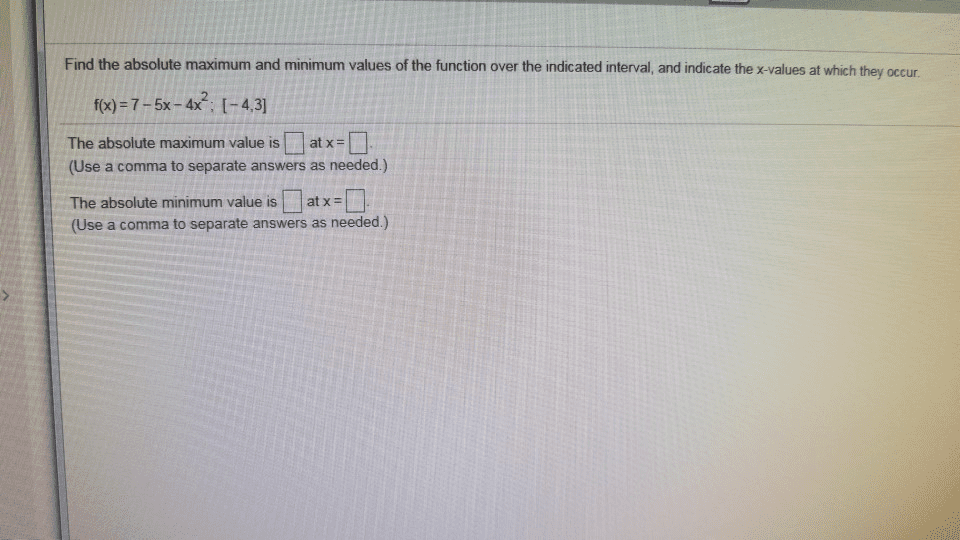
Find the absolute maximum and minimum values of the function over the indicated interval, and indicate the x-values at which they occur f(x) 7-5x-4x -4,3] The absolute maximum value isâ¡ate-D (Use a comma to separate answers as needed.) The absolute minimum value isâ¡atx:D (Use a comma to separate answers as needed.)
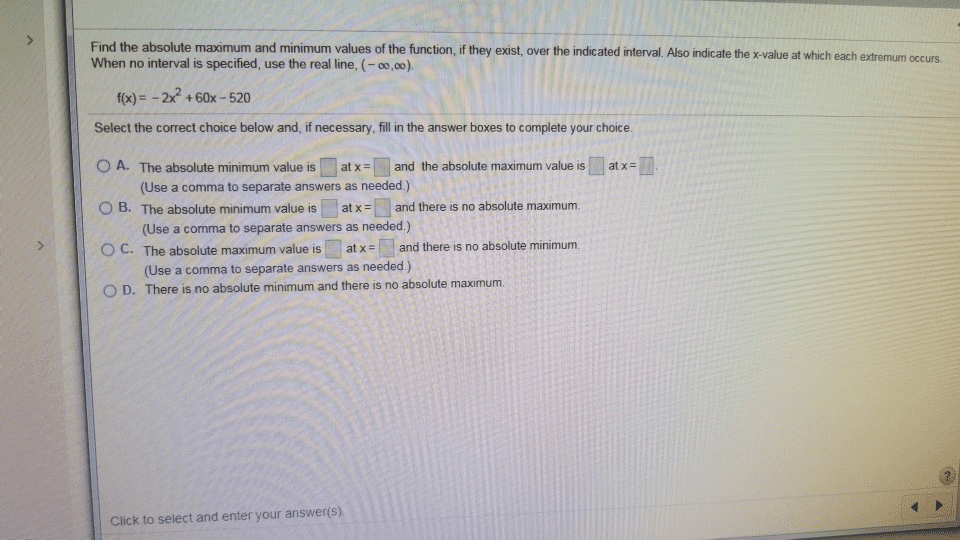
Find the absolute maximum and minimum values of the function, if they exist, over the indicated interval. Also indicate the x-value at which When no interval is specified, use the real line, (-o0,00) fx)2x+60x-520 Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. ãA. The absolute minimum value is at x and the absolute maximum, value at x OB. The absolute minimum value is matx- and there is no absolute maximum. O C. The absolute maximum value is atx and there is no absolute minimum. O D. There is no absolute minimum and there is no absolute maximum. (Use a comma to separate answers as needed.) se a comma to separate answers as needed.) a comma to separate answers as needed.) (Use Click to select and enter your answer(s)
Find the absolute extrema of the function, if they exist, over the indicated interval. Also indicate the x-value at which each extremum occurs. If use the real numbers, (-oo,o0). no interval is specified, fx)- (x-3) Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. 0 A. The absolute maximum is â¡ at x-U and the absolute minimumisE at x- O B. The absolute maximum is atxand there is no absolute minimum O C. The absolute minimum isatx and there is no absolute maximum. O D. There is no absolute maximum and no absolute minimum. Use a comma to separate answers as needed.) (Use a comma to separate answers as needed.) (Use a comma to separate answers as needed) Glick to select and enter your answer(s)
Show transcribed image text