HomeStudy Guides420,000US230,000

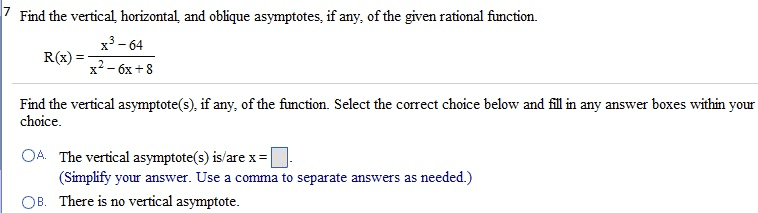
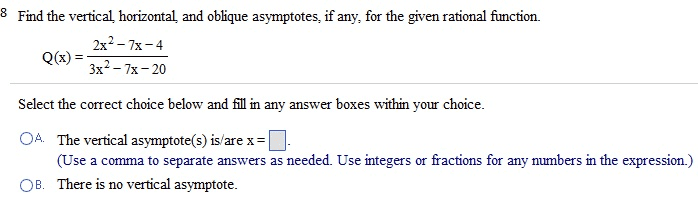
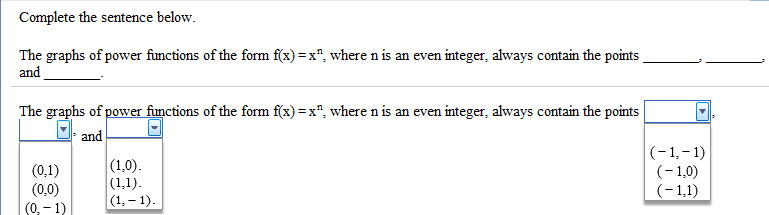MATH 411 : MATH411_BOYLE-M_FALL2011_0101_MID_EXAM

6 views2 pages

turquoisegnu128

10 Jan 2019

School

University of Maryland

Department

Course

Professor

For unlimited access to Study Guides, a Grade+ subscription is required.

Document Summary

Math 411 fall 2011 boyle exam 1: (10 points) a metric space is a set x together with a real- valued function d de ned on pairs of points (x, y) from x. Prove that f has directional derivatives in every direction at (0, 0). (20 points) let h = {(x, y) r2 : y = 0}, the hori- Suppose f : r2 r2 is continuous and there are sequences pn and qn in h such that limn f (pn) = 0 and limn ||f (qn)|| = . Suppose also the partial derivative functions are bounded: there is a positive number m such that | f. Y (p)| m at every point p in r2. 7. (25 points) for each of the following, answer true or. A function f : rn r is continuously di erentiable if it a. is di erentiable and in addition it is continuous.

Related textbook solutions

Calculus

ISBN: 9781319050733

Single Variable Calculus: Early Transcendentals

4th Edition, 2018

ISBN: 9781337687805

CALCULUS:EARLY TRANSCENDENTALS

ISBN: 9781319050740

Related Documents

MATH 411 Midterm: MATH411 BOYLE-M FALL2011 0101 MID EXAM

turquoisegnu128

MATH 411 Midterm: MATH411 BOYLE-M FALL2011 0101 MID SOL

turquoisegnu128

MATH 411 Lecture Notes - Tangent Space, Closed Set, Lipschitz Continuity

turquoisegnu128

Related Questions

6. On the axis below, sketch the graph of a continuous function y = f(:) having all of the following properties. Points are awarded for accuracy and neatness. [12 points) (i) f(0) = 3 and f(3) = 0 (ii) f'(-2) = f '(1) = 0 (iii) f is not differentiable at r=-1 (iv) [(x) > 0 for all & € (-0,3) (v) lim f(x) = 0 and lim,- S(:) = -1 (vi) F"(x) > 0 for all x € (-20, -3) and f "(c) < 0 for all 2 € (-1,2) (vii) (-3,2) is a point of inflection of f

+ 1. In all of this question let f(x) = + (a) Find f'(x) and simplify. [4 points) (b) Find the equation of the tangent line to the curve y = f(x) that is parallel to the line 110 + 64y = 75 and whose point of tangency (C,y) satisfies x, y > 0. Give your answer in the form Ac + By = C where A, B, C are integers and A >0.R [7 points) (c) Assume g is a differentiable function such that g(0) = g(2) = 9' (2) = 2 and g'(0) = 4. Find A when x = 0 where A(x) = g(x)g(f(x)). 15 points)

Algebra

Complete the sentence below. If r is a real zero of even multiplicity of a function f then the graph of f the x-axis at r. If r is a real zero of even multiplicity of a function f then the graph of f the x-axis at r. Complete the sentence below. The graphs of power functions of the form f(x) = x n: where n is an even integer, always contain the points and The graphs of power functions of the form f(x) = x n: where n is an even integer, always contain the points and If r is a solution to the equation f(x) = 05 name three additional statements that can be made about f and r assuming f is a polynomial function. Choose the correct answer below. If r is a solution to the equation f(x) = 0, then r is a real zero of the polynomial function r is an x-intercept of the graph of and x - r is a factor of f. If r is a solution to the equation f(x) = 0, then r is a complex zero of the polynomial function r is an x-intercept of the graph of and x + r is a factor of f. If r is a solution to the equation f(x) = 0, then r is a real zero of the polynomial function r is a y-intercept of the graph of x and x + r is a factor of f. Explain what the notation Km f(x) = -infinity means. x rightarrow infinity Choose the correct answer below. The limit of f(x) as x approaches - infinity equals infinity. The limit of x as f(x) approaches infinity equals - infinity. The limit of f(x) as x approaches infinity equals - infinity. The limit of x as f(x) approaches - infinity equals infinity. Form a polynomial whose zeros and degree are given. Zeros: -7, multiplicity 1; - 3, multiplicity 2; degree 3 Type a polynomial with integer coefficients and a leading coefficient of 1 in the box below. F(x) = Find the vertical horizontal and oblique asymptotes, if any, for the following rational function.R(x) = 12x / x + 20 Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Use a comma to separate answers as needed.) There is no vertical asymptote. Find the vertical, horizontal and oblique asymptotes, if any, of the given rational function. R(x) = x3 - 64 / x2 - 6x + 8 Find the vertical asymptote(s), if any, of the function. Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Simplify your answer. Use a comma to separate answers as needed.) There is no vertical asymptote. Find the vertical, horizontal and oblique asymptotes, if any, for the given rational function. Q(x) = 2x2 - 7x - 4 / 3x2 - 7x - 20 Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Use a comma to separate answers as needed. Use integers or fractions for any numbers in the expression.) There is no vertical asymptote. Analyze the graph of the function. R(x) = x + 14 / x(x + 15) What is the domain of R(x)? {x x 0 andx - 16} {x x 0 andx - 16 andx - 14} {x x 0 and x - 14} All real numbers Analyze the graph of the function. R(x) = 5x + 5 / 4x + 12 What is the domain of R(x)? {x|x 0 and x -3 and x - 1} {x|x -3} {x|x and x - 3} All real numbers Analyze the graph of the function.R(x) = x2 / x2 + x - 56 What is the domain of R(x)? {x|x 7 and x - 8} {x|x 0,x -1, and x 8} {x|x 0, x 7, and x - 8} All real numbers

Show transcribed image text Complete the sentence below. If r is a real zero of even multiplicity of a function f then the graph of f the x-axis at r. If r is a real zero of even multiplicity of a function f then the graph of f the x-axis at r. Complete the sentence below. The graphs of power functions of the form f(x) = x n: where n is an even integer, always contain the points and The graphs of power functions of the form f(x) = x n: where n is an even integer, always contain the points and If r is a solution to the equation f(x) = 05 name three additional statements that can be made about f and r assuming f is a polynomial function. Choose the correct answer below. If r is a solution to the equation f(x) = 0, then r is a real zero of the polynomial function r is an x-intercept of the graph of and x - r is a factor of f. If r is a solution to the equation f(x) = 0, then r is a complex zero of the polynomial function r is an x-intercept of the graph of and x + r is a factor of f. If r is a solution to the equation f(x) = 0, then r is a real zero of the polynomial function r is a y-intercept of the graph of x and x + r is a factor of f. Explain what the notation Km f(x) = -infinity means. x rightarrow infinity Choose the correct answer below. The limit of f(x) as x approaches - infinity equals infinity. The limit of x as f(x) approaches infinity equals - infinity. The limit of f(x) as x approaches infinity equals - infinity. The limit of x as f(x) approaches - infinity equals infinity. Form a polynomial whose zeros and degree are given. Zeros: -7, multiplicity 1; - 3, multiplicity 2; degree 3 Type a polynomial with integer coefficients and a leading coefficient of 1 in the box below. F(x) = Find the vertical horizontal and oblique asymptotes, if any, for the following rational function.R(x) = 12x / x + 20 Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Use a comma to separate answers as needed.) There is no vertical asymptote. Find the vertical, horizontal and oblique asymptotes, if any, of the given rational function. R(x) = x3 - 64 / x2 - 6x + 8 Find the vertical asymptote(s), if any, of the function. Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Simplify your answer. Use a comma to separate answers as needed.) There is no vertical asymptote. Find the vertical, horizontal and oblique asymptotes, if any, for the given rational function. Q(x) = 2x2 - 7x - 4 / 3x2 - 7x - 20 Select the correct choice below and fill in any answer boxes within your choice. The vertical asymptote(s) is/are x = (Use a comma to separate answers as needed. Use integers or fractions for any numbers in the expression.) There is no vertical asymptote. Analyze the graph of the function. R(x) = x + 14 / x(x + 15) What is the domain of R(x)? {x x 0 andx - 16} {x x 0 andx - 16 andx - 14} {x x 0 and x - 14} All real numbers Analyze the graph of the function. R(x) = 5x + 5 / 4x + 12 What is the domain of R(x)? {x|x 0 and x -3 and x - 1} {x|x -3} {x|x and x - 3} All real numbers Analyze the graph of the function.R(x) = x2 / x2 + x - 56 What is the domain of R(x)? {x|x 7 and x - 8} {x|x 0,x -1, and x 8} {x|x 0, x 7, and x - 8} All real numbers

indigosardine988