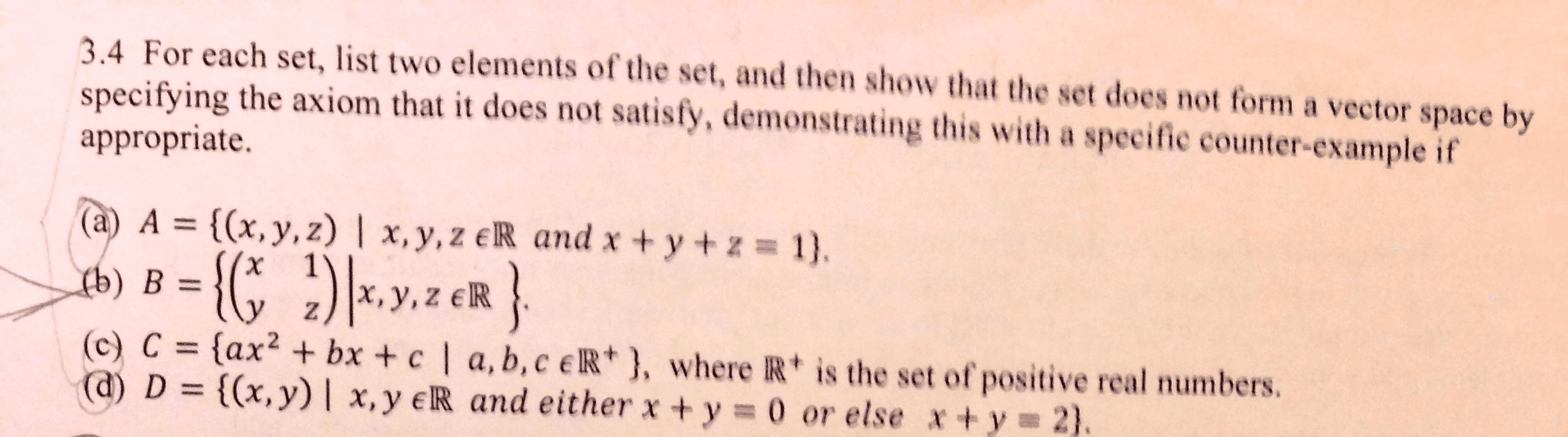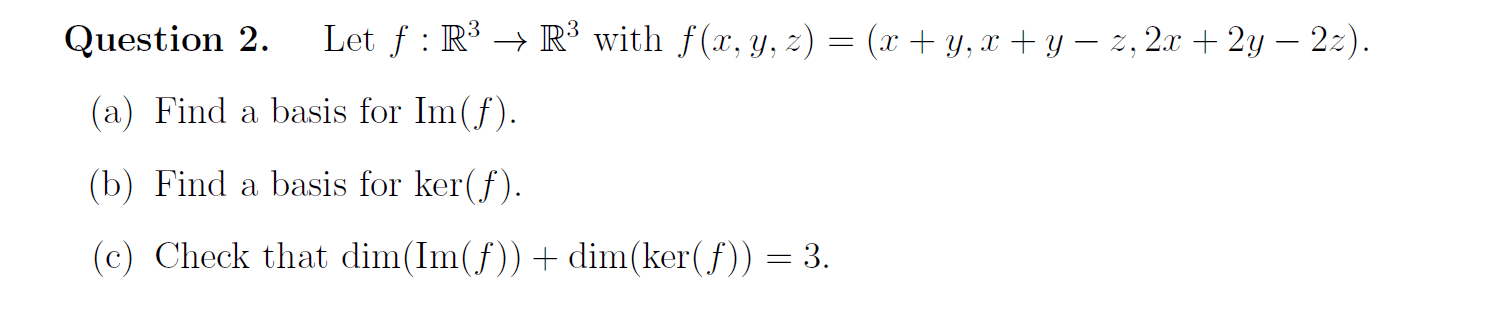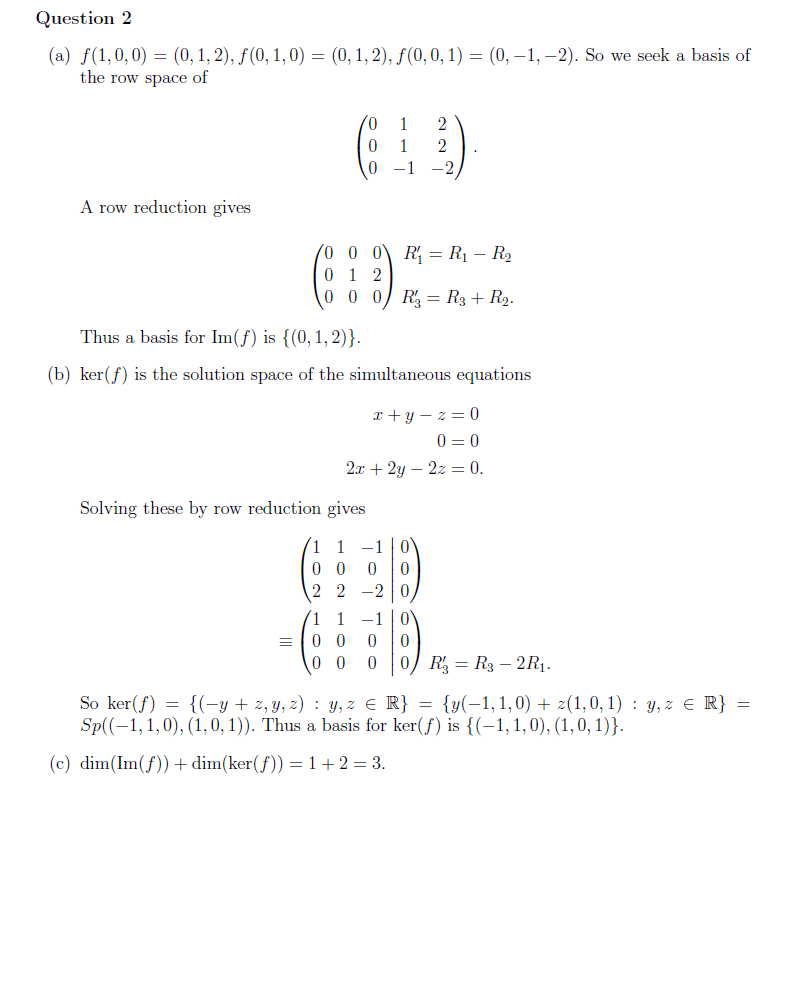MATH 411 Lecture Notes - Tangent Space, Closed Set, Lipschitz Continuity
Document Summary
Math 411 fall 2011 boyle exam 1: (10 points) a metric space is a set x together with a real- valued function d de ned on pairs of points (x, y) from x. State the axioms that d must satisfy for x to be a metric space. For vectors x, y in rn: (we only considered this inequality for rn. But it applies to any vector space with a scalar product. ) It means that there exist real numbers a, b such that lim (x,y) (x0,y0) f (x, y) f (x0, y0) a(x x0) b(y y0) p(x x0)2 + (y y0)2. = 0 . (this is one of the possible notations for this limit. ) When such num- bers a, b exist, it can only be that a = f. X(x0, y0) and b = f: (20 points) de ne the function f from r2 to r by the rule f (x, y) = sin(y2/x)px2 + y2.