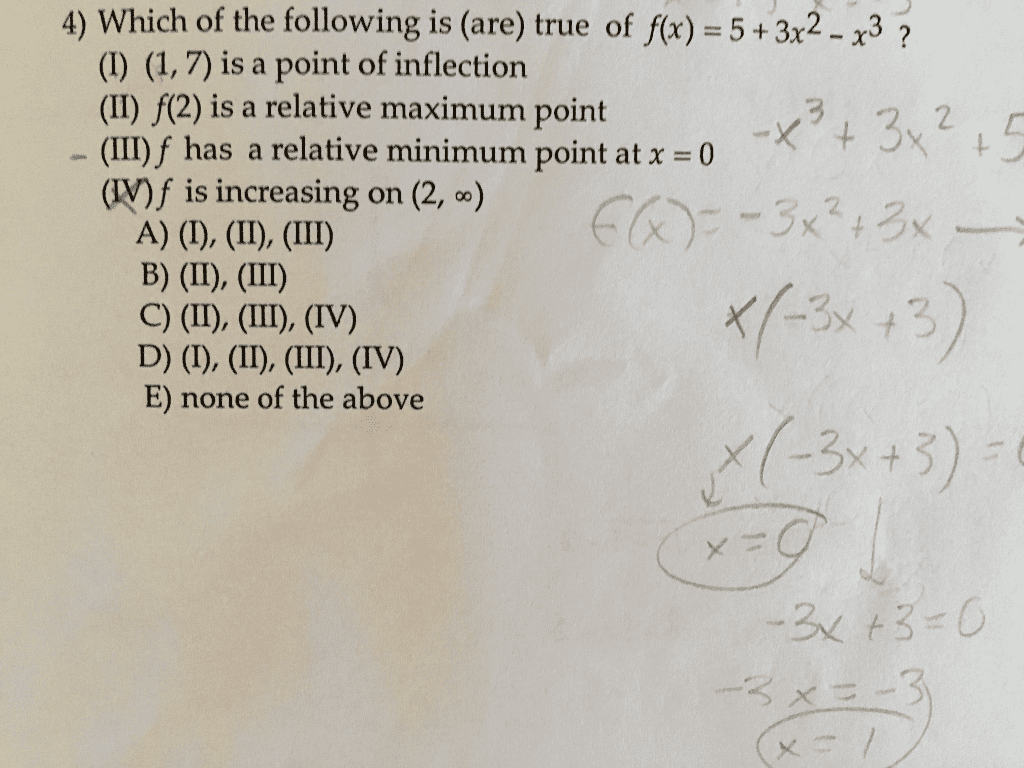MATH 251 Midterm: MATH 251 TAMU 251-Spring 11 Exam 2s11 Solutions
Document Summary
Which of the following statements is true: f (x, y) has a local minimum at (x, y) = ( 2, 2). Ii. f (x, y) has a critical point at (x, y) = (1, 2). Iii. f (x, y) has a saddle point at (x, y) = (0, 6). (a) i only (b) iii only (c) i and ii only (d) i and iii only (e) ii and iii only. For i, we see from the table that ( 2, 2) is a critical point since fx( 2, 2) = 0 and fy( 2, 2) = 0, so we try the second. Derivative test to determine which kind of critical point it is. We calculate d = fxx( 2, 2)fyy( 2, 2) fxy( 2, 2)2 = 4 1 = 3 > 0 and observe fxx( 2, 2) = 2 < 0, so f has a local maximum at ( 2, 2).