Question

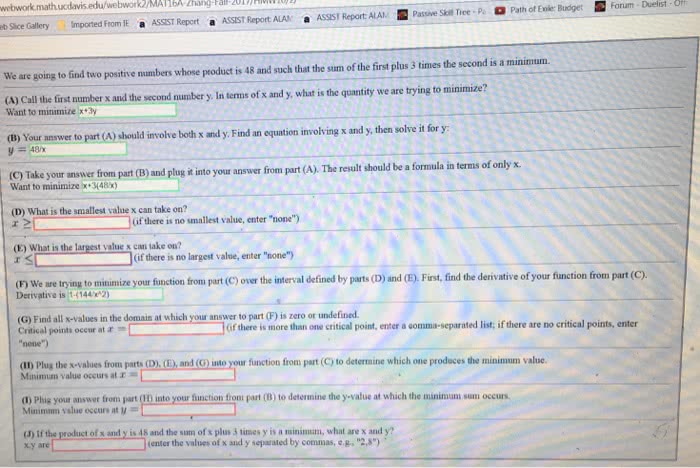
Centerville is the headquarters of Greedy Cablevision Inc. The cable company is about to expand service to two nearby towns, Springfield and Shelbyville. There needs to be cable connecting Centerville to both towns. The idea is to save on the cost of cable by arranging the cable in a Y-shaped configuation.

Centerville is located at (7,0) in the xy-plane, Springfield is at (0,6), and Shelbyville is at (0,-6). The cable runs from Centerville to some point (x,0) on the x-axis where it splits into two branches going to Springfield and Shelbyville. Find the location (x,0) that will minimize the amount of cable between the 3 towns and compute the amount of cable needed. Justify your answer.

To solve this problem we need to minimize the following function of x:

1) f(x)=
2) We find that f(x) has a critical number at x=

3) To verify that f(x) has a minimum at this critical number we compute the second derivative f??(x) and find that its value at the critical number =_____ , a positive number.

4) Thus the minimum length of cable needed =

please show all work Thanks