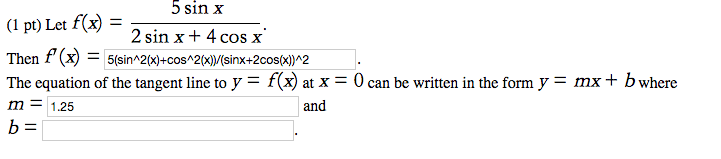MAT 307 Midterm: MAT 307 SBU Fall 10 Exam 2Solutions
31 Jan 2019
School
Department
Course
Professor
Document Summary
Solutions to midterm 2: let f (x, y) = cos(x) sin(x2 + y2). Calculate the gradient of f when x = 0 and y = F (x, y) = (cid:10)2x cos(x) cos(x2 + y2) sin(x) sin(x2 + y2), 2y cos(x) cos(x2 + y2)(cid:11) 2e. (recall that sin(0) = 0, cos(0) = 1, and cos( /4) = 1/ 2. ) Write the equation of the plane tangent to the surface z = f (x, y) at the point(cid:18)0, Solution: recall that the plane tangent to a surface z = f (x, y) satis es the equation z = z0 + fx(x x0) + fy(y y0). In the current case, we have z = A particle is moving along the curve (t) = (cid:28) . 2 change of f (x, y) along this curve when t = /2. cos t, Solution: this means we want to nd the directional derivative in the direction of the tan- gent to (t) at t = /2.
