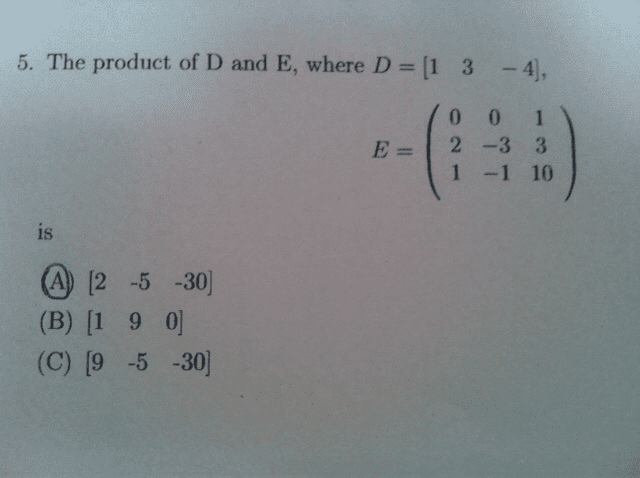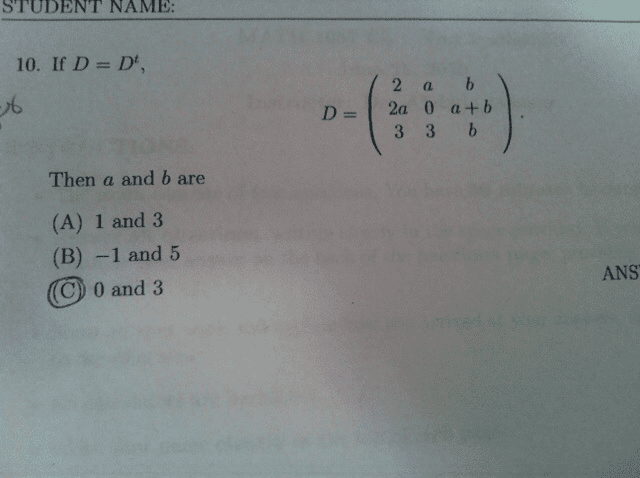MATH 3000 Final: MATH 331 Mizzou Final Exam
Document Summary
Math 331 sample exam 1 brief solutions: the reduced row-echelon form of the matrix is . The solutions are any vector of the form. 0 ]t , where : (10 points) a 1 = . Put another way, the augemented matrix has a leading one in the last column. 6: true. det(a) = det(at ) = 2 6= 0 so a is invertible, false. The system ax = 0 is always consistent. Example 0x1 = 0 is consistent, but 0x1 = 1 is not, e. g. , take a = [0], and b = [1]: false. The easy example is to take b to be the matrix of all 0"s. But even if i had said b was not the 0 matrix, it would still be false. Take b to be any singular matrix and you will be able to nd a and c that work. A(y + z) = ay + az = b + 0 = b: true.