MATH 3000 Midterm: MATH 331 Mizzou Exam 3
Document Summary
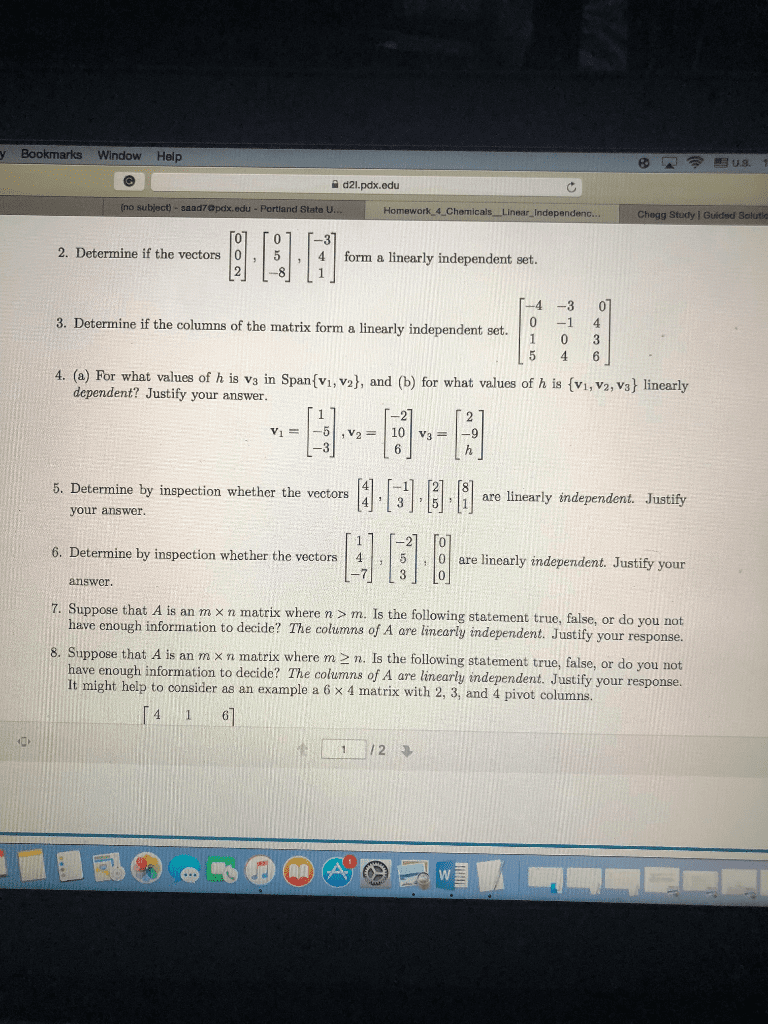
The problem is that these vectors are not linearly independant. Making a 5 4 matrix and row reducing will give 3 leading 1"s in the rst three columns. Thus s is not a subspace: a) dim(r2 3) = 2 3 = 6. Then det(a) = 13 6= 0, so the set is a basis for r3, hence is linearly independent: the set contains the 0 vector, so must be linearly dependent (e. g. , 0(1 + x 6x3) + 0(x2 + 3), +1(0) + 0(x 1) = 0, even though not all coe cients are 0): when you row reduce you will get 3 leading 1"s, so rank(a) = 3. {(1, 0, 1, 0, 2), (0, 1, 3, 0, 0), (0, 0, 0, 1, 2)}. The rst, second and fourth columns of a are a basis for col(a). 0(cid:21) = 12 6= 0, so the columns are a basis for r2.