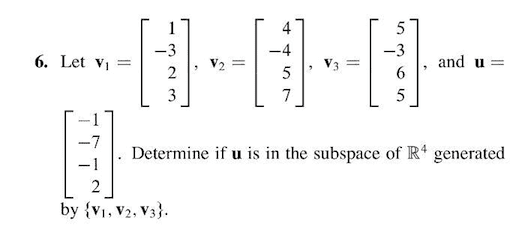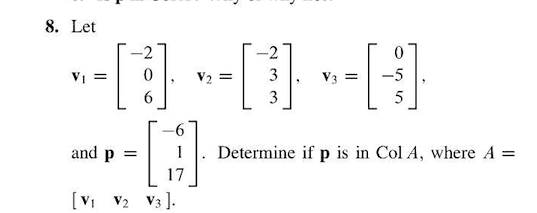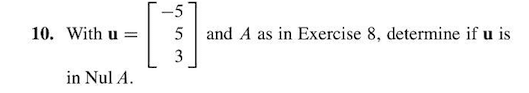MATH-205 Midterm: Bates MATH 205 041305jayawant205exam
Document Summary
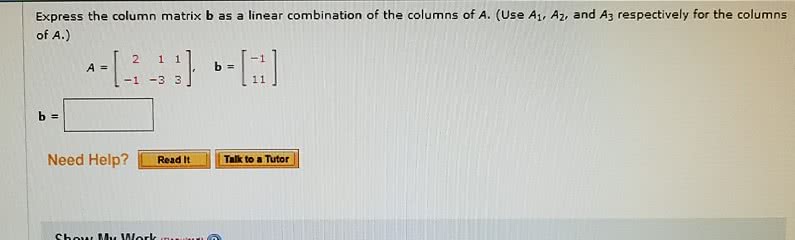
Name: check that you have 9 questions on four pages, show all your work to receive full credit for a problem, (10 points) let a = Use this matrix to answer the following questions: (a) find a basis for col a. Explain: (10 points) let ~p1(t) = 1 t2, ~p2(t) = t t2, ~p3(t) = 2 2t + t2. (a) use coordinate vectors to show that b ={~p1, ~p2, ~p3} is a basis for p2. ~q in p2, given that [q]b = . 1 (b) de ne a linear transformation t : p2 r2 by t (a0 + a1t + a2t2) = (cid:20) a0 a1 + a2 (cid:21). T (~p1), t (~p2), and t (~p3). (c) for the linear transformation t de ned in part (b), the kernel of t is a subspace of p2 of dimension one. Find a basis for the kernel of t . (your answer to part (b) can help you to nd a basis. )