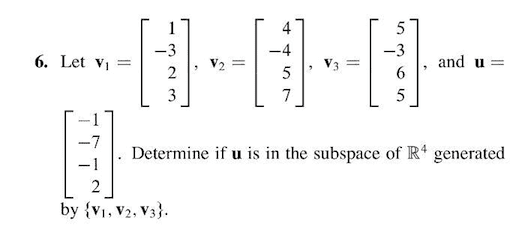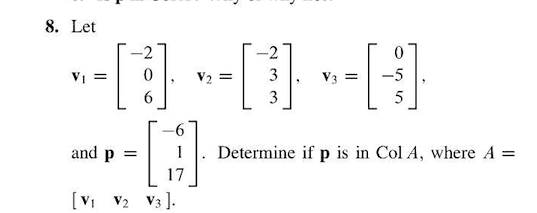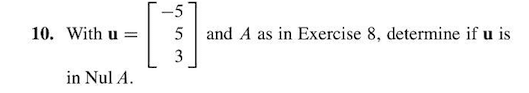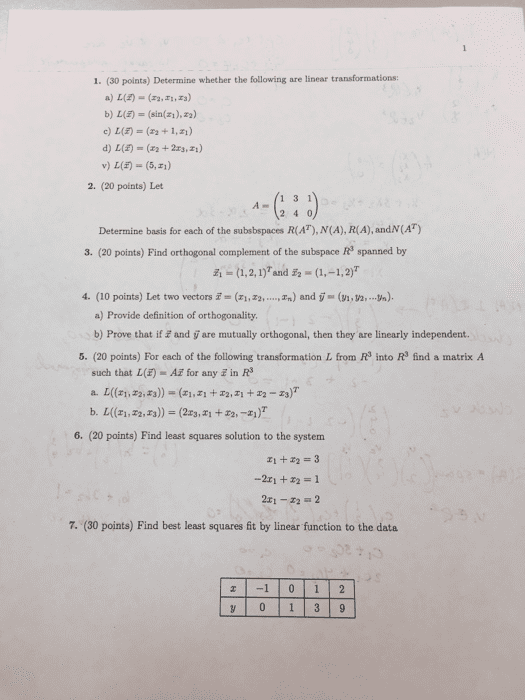MATH-205 Midterm: Bates MATH 205 031805jayawant205exam
Document Summary
Name: check that you have 6 questions on two pages, show all your work to receive full credit for a problem, (9 points) let a = (cid:20) 1 3 2. Use this matrix to answer the following questions: (a) find a basis for col a. (b) col a is a subspace of r2. Explain: (7 points) let v be a vector space of dimension three. The vectors ~v1, ~v2, ~v3, and ~v4 in v are such that span{~v1, ~v2, ~v3, ~v4 } = v , and ~v1 + 3~v2 2~v3 + ~v4 = ~0. Explain how the basis you nd satis es the two conditions in the de nition of a basis: (8 points) a homogeneous system of seven linear equations in eight unknowns has one free variable. Explain: (8 points) let b be the basis of p2 consisting of the polynomials 1 t2, t t2, and 2 2t + t2.