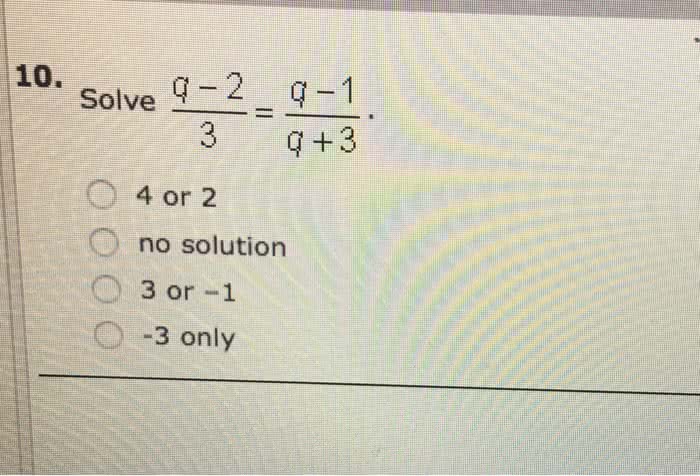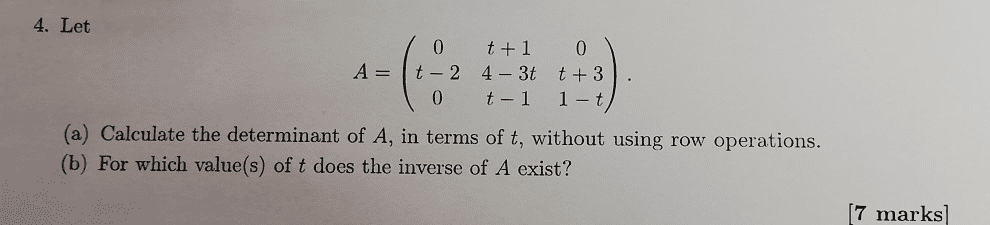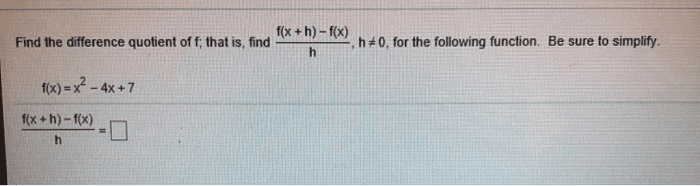zumjhoo
Indian Institute of Technology - IIT Delhi
0 Followers
0 Following
0 Helped
Physicist.
zumjhooLv6
26 Sep 2022
Answer:1 ) we know the slope-intercept form of a straight line is y = mx+c. Fr...
zumjhooLv6
26 Sep 2022
1) let 2) let 3) let 4) let
zumjhooLv6
26 Sep 2022
Answer: For infinite solution rank of the matrix should be less than the no. o...
zumjhooLv6
26 Sep 2022
Answer: Please see the attachment below
zumjhooLv6
26 Sep 2022
Answer: If ax3+bx2+cx+d=0 then By putting values in a,b,c, and d we will get t...
zumjhooLv6
26 Sep 2022
Answer: If ax3+bx2+cx+d=0 then By putting values in a,b,c, and d we will get t...
zumjhooLv6
11 Sep 2022
Answer: x = 2,3
zumjhooLv6
11 Sep 2022
Answer: 1) 1 + 5 x + 10 x^2 + 10 x^3 + 5 x^4 + x^5 2) -1 + 5 x - 10 x^2 + 10 x...
zumjhooLv6
11 Sep 2022
Answer: density = mass/ volume = m/V
zumjhooLv6
11 Sep 2022
Answer:
zumjhooLv6
11 Sep 2022
Answer: 3*1 + 10/7 = 31/7 = 4.428
zumjhooLv6
11 Sep 2022
Answer: r = 1- a/s
zumjhooLv6
11 Sep 2022
Answer: Invalid equation. Both sides are p present which cancels each other an...
zumjhooLv6
11 Sep 2022
Answer: y = 3, 6
zumjhooLv6
11 Sep 2022
Answer: n(n-1)(n-2)
zumjhooLv6
11 Sep 2022
Answer: q = -1, or 3
zumjhooLv6
11 Sep 2022
Answer: Please see the attachment below
zumjhooLv6
11 Sep 2022
Answer:
zumjhooLv6
11 Sep 2022
Answer: y = 1.5x + 2.7
zumjhooLv6
11 Sep 2022
Answer: y = 0.5x +1.5
zumjhooLv6
11 Sep 2022
Answer:
zumjhooLv6
11 Sep 2022
Answer: a) 2 - t - 2 t^2 + t^3 b) Inverse won't exist for the root of the firs...
zumjhooLv6
11 Sep 2022
Answer:
zumjhooLv6
11 Sep 2022
Answer: x = 5
zumjhooLv6
11 Sep 2022
Answer: Given Q + P =10 Q + 2P = 12 On solving these equations P = 2 and Q = 8
zumjhooLv6
11 Sep 2022
Answer: Mount Everest
zumjhooLv6
11 Sep 2022
Answer: Mount Everest
zumjhooLv6
11 Sep 2022
Answer: Th rate of change of y with respect to x is
zumjhooLv6
11 Sep 2022
Answer: Equation of straight line passing through two points (x1,y1), (x2,y2) ...
zumjhooLv6
11 Sep 2022
Answer: common multiple = 4w^7x^3
zumjhooLv6
11 Sep 2022
Answer: Given p= 0.4q p/0.4 = q q = 2.5p q is 250% of p
zumjhooLv6
11 Sep 2022
Answer: L.H.S.
zumjhooLv6
11 Sep 2022
Answer: It's the algebraic identity (q-m)(q+m) = q^2 - m^2
zumjhooLv6
11 Sep 2022
Answer: Put the value of u and t and solve tu + u = -0.78
zumjhooLv6
11 Sep 2022
Answer: n = 1.41667
zumjhooLv6
11 Sep 2022
Answer: x = -1 y = 3
zumjhooLv6
11 Sep 2022
Answer:
zumjhooLv6
11 Sep 2022
Answer: x = -2, y = 5, z = 4
zumjhooLv6
11 Sep 2022
Answer: Just put (x+h) at the place of x for f(x+h) and solve
zumjhooLv6
11 Sep 2022
Answer: 8) 9 9) -3 10) 12