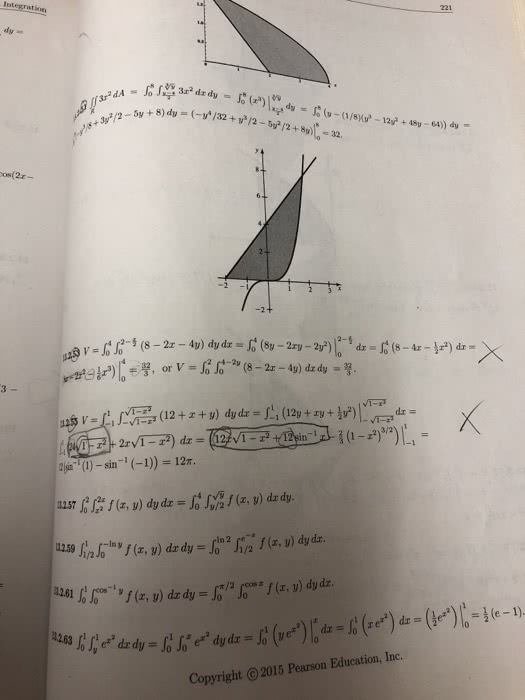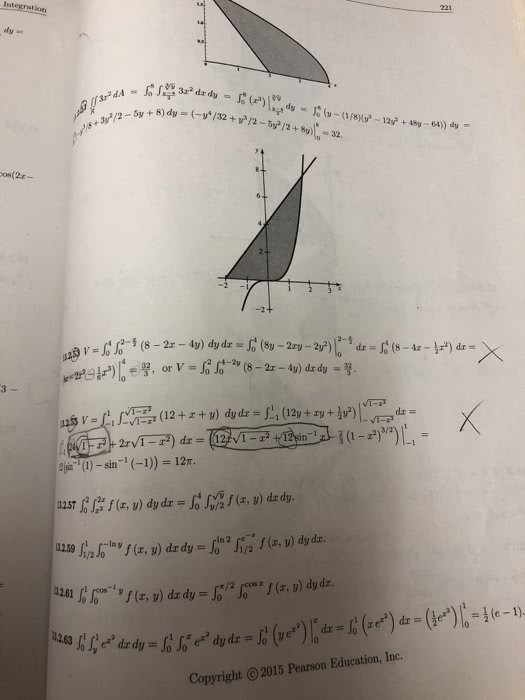L24 Math 233 Lecture 26: Math 233 – Lecture 26 – Double Integrals
L24 Math 233 verified notes
26/34View all
Document Summary
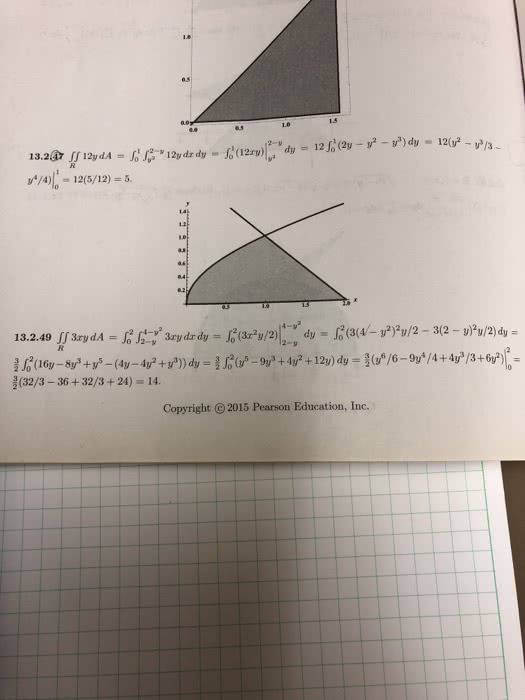
Math 233 lecture 26 double integrals. Fubini"s theorem if f is continuous on the rectangle r = [a,b] [c,d], then. A b c f(x,y) dxdy = 0 d f(x,y) dydx = c. R 0 d a: you should always remember to change the order of the integrals to correspond to the sequence of dx and dy. Example 1 find the volume of the solid bounded by x2+2y2+z = 16, x=2, y=2, and the 3 coordinates f = z = 16-x2-2y2. Double integrals over general regions: we consider 2 kinds of regions b g1 g2 f(x,y) dydx type i: every x value exists on the interval [a,b], but not all y values lie within the boundary. D can be written as d = {(x,y) | a x b, g1(x) y g2(x)} Where g1(x) and g2(x) are continuous in [a,b] V = a type ii: every y value exists on the interval [c,d], but not all x values lie within the boundary.