L24 Math 233 Lecture Notes - Lecture 21: Multivariable Calculus, Minimax, Fxx
L24 Math 233 verified notes
21/34View all
Document Summary
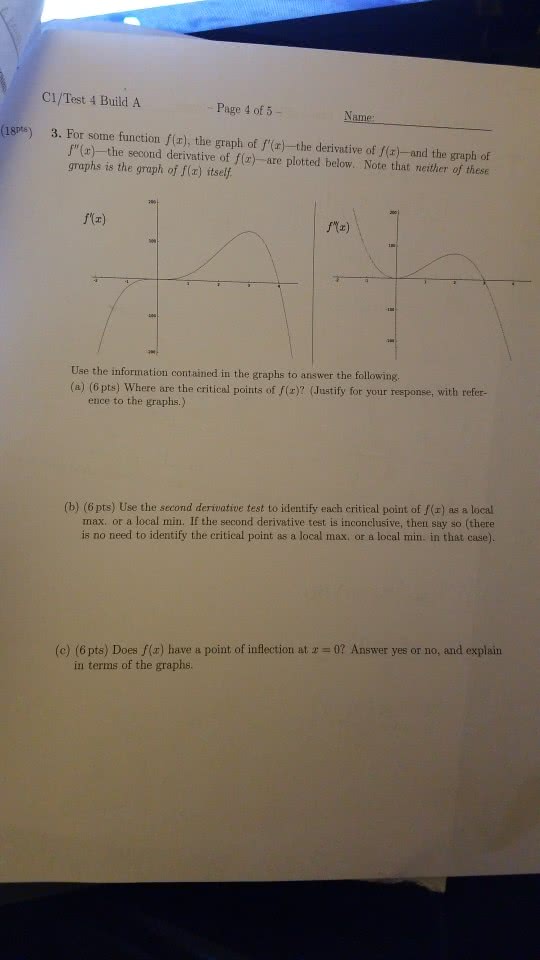
Math 233 lecture 21 local max & min. Single-variable calculus: we work locally: when there is a max/min, the value at that point is greater/less than that of points near it, global max/min. A close interval is necessary in most cases. To find the global max/min, check the values at critical points and boundaries: local max/min. When the first derivative equals 0 or is undefined, there is a critical point. Use the second derivative to check if there is a max or min at critical points. Theorem #1 if f has a local max/min at (a,b), then (a,b) is a critical point for f: no vice-versa !! You can never say if there is a critical point for f at (a,b), there is a local max/min : example. Find all critical points for f(x,y) = x2+y4+2xy fx = 2x+2y fy = 4y3+2x. 2x = -2y substitute 2x = -2y for 4y3+2x, we get.