MATH 1131Q Lecture Notes - Lecture 8: Maxima And Minima, Asymptote

• School: UConn
• Department: Mathematics
• Course: MATH 1131Q
• Professor: Amit Savkar

Document Summary

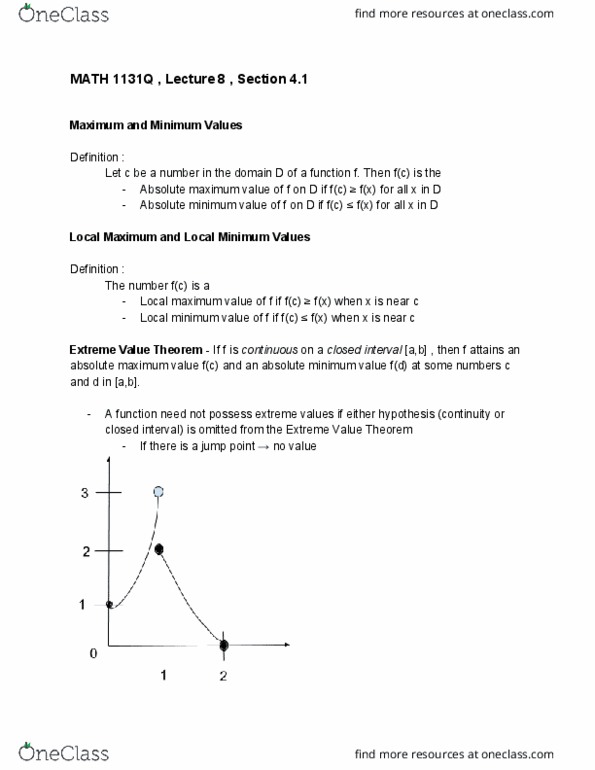
Math 1131q , lecture 8 , section 4. 1. Let c be a number in the domain d of a function f. then f(c) is the. Absolute maximum value of f on d if f(c) f(x) for all x in d. Absolute minimum value of f on d if f(c) f(x) for all x in d. Local maximum value of f if f(c) f(x) when x is near c. Local minimum value of f if f(c) f(x) when x is near c. If f is continuous on a closed interval [a,b] , then f attains an. Extreme value theorem - absolute maximum value f(c) and an absolute minimum value f(d) at some numbers c and d in [a,b]. A function need not possess extreme values if either hypothesis (continuity or closed interval) is omitted from the extreme value theorem. If there is a jump point no value ie. min value f(2)=0 , no maximum value.