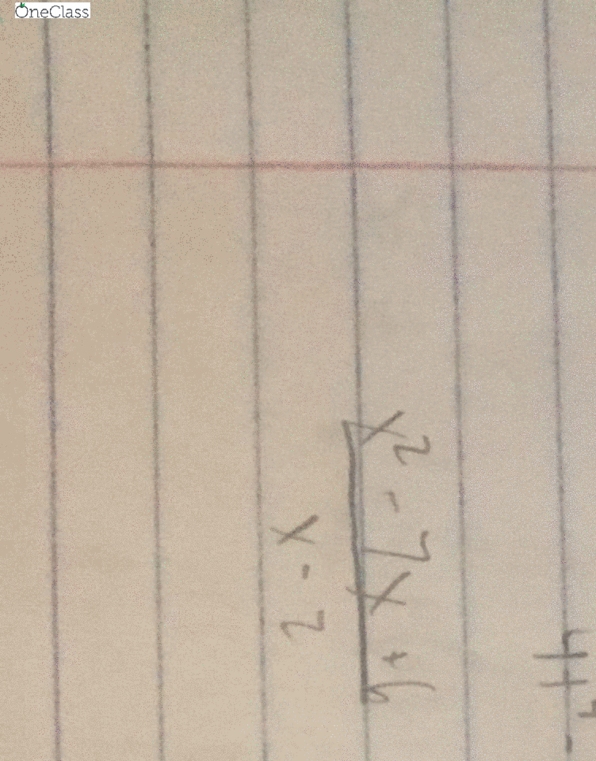MATH 1131Q Lecture Notes - Lecture 3: Exponential Function, Power Rule, Differentiable Function
MATH 1131Q verified notes
3/15View all
Document Summary
Math 1131q , lecture 3 , section 2. 7/2. 8/3. 1. Definition of a limit - time f"(a) lim f (a + h) - f (a) The change in x is x = x2 - x1. Y = f(x2) - f(x1) is called the average rate of change of y with respect to x. The derivative as a function lim y = lim f(x2) - f(x1) When graphing the derivative; look at the graph of the original function. Where the slope is negative, the derivative graph will be on the negative y-axis. And where the slope is positive, the derivative will be graphed on the positive y-axis. A function is differentiable if f"(x) exists. A function can be continuous, but not differentiable. But it cannot be differentiable if it is not continuous. Examples when a function can be continuous, but not differentiable. Theorem : if f is differentiable at a , then f is continuous at a.
