MAT 21B Lecture 13: MAT 21B – Lecture 13 – The Surface Area of Any Surface of Revolution

MAT 21B – Lecture 13 – The Surface Area of Any Surface of Revolution
• The reasoning behind the surface area of any surface of revolution is more
complicated because in the
o Language of approximations, the limits of sums that are not definite
integrals will appear. For example,
o Language of differentials, f(x)dx2 = 0 where dx2 = 0.
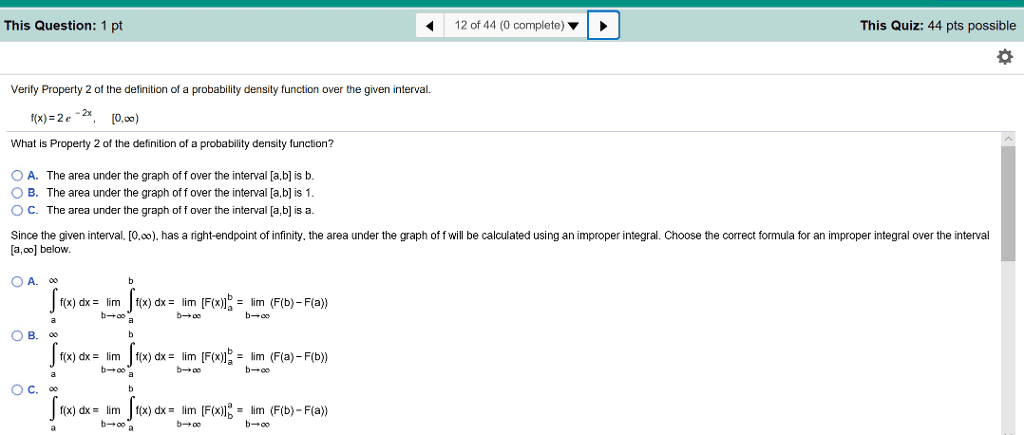
• Example of
with a = 0 and b = 2 and a given
function, f(x) shown in the table below:
Function, f(x)
Limit of the sums with
f(x) = x
f(x) = x2
f(x) = x3
These examples above demonstrated that because
is squared, then the
denominator has a higher degree of polynomial. As a result, the denominator
gets bigger faster as n than the numerator. Thus, the limit of sum 0.
• Example: Set up a definite integral equal to the surface area of the surface, S
obtained by revolving the curve, C that is the graph of f(x) = sin(x) on [0, 1] about
the x – axis.

83
MAT 21B Full Course Notes
Verified Note
83 documents