MATH 154 Lecture Notes - Lecture 19: Maxima And Minima, Differentiable Function

• School: Simon Fraser University
• Department: Mathematics
• Course: MATH 154
• Professor: Yusuf Tuncer

Document Summary

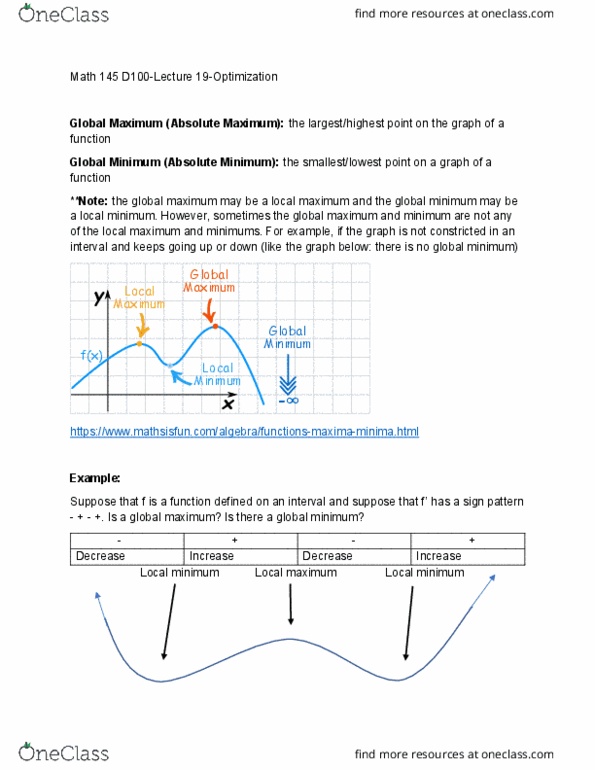
Global maximum (absolute maximum): the largest/highest point on the graph of a function. Global minimum (absolute minimum): the smallest/lowest point on a graph of a function. **note: the global maximum may be a local maximum and the global minimum may be a local minimum. However, sometimes the global maximum and minimum are not any of the local maximum and minimums. For example, if the graph is not constricted in an interval and keeps going up or down (like the graph below: there is no global minimum) https://www. mathsisfun. com/algebra/functions-maxima-minima. html. Suppose that f is a function defined on an interval and suppose that f" has a sign pattern. This function may not have a global maximum because it keeps going up. If so, where? f(x)=-(x2-6x+4) use x=(-b+- (b2-4ac))/2a x=(-(-6)+- (-6)2-4(1)(4))/2(1) x=(6+- (36-16))/2 x=(6+- 20)/2 x=(6+- (2x2x5))/2 x=(6+-2 5)/2 x=3+- 5. The function has a global maximum at x=3. F =-2<0 therefore, there must be a local maximum.