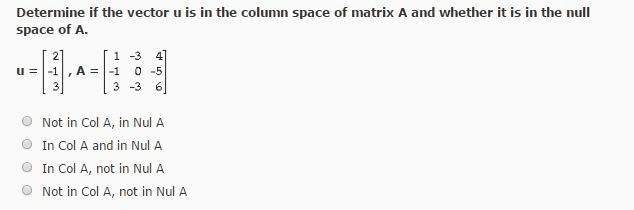MATH 415 Study Guide - Final Guide: Null Character, Orthogonal Complement, Linear Map

• School: University of Illinois
• Department: Mathematics
• Course: MATH 415
• Professor: J Li

Document Summary

Let a be an m n matrix. The left null space of a is the orthogonal complement of the column space of a, so the inner product of any vector from the rst space and a vector from the second space is 0. So whenever x is in the left null space of a and y is in the column space of a, then x y = 0. There is no relation between the spaces in the other answers. Thus there is a matrix a and a non-zero vector x such that x is both in the column space of a and in the null space of a. Note that (cid:20)1 and vectors x, y such that x is in the column space of a and y is in the row space of a and x y 6= 0. 1(cid:21) is both in the column space and in the row space of (cid:20)1 1.