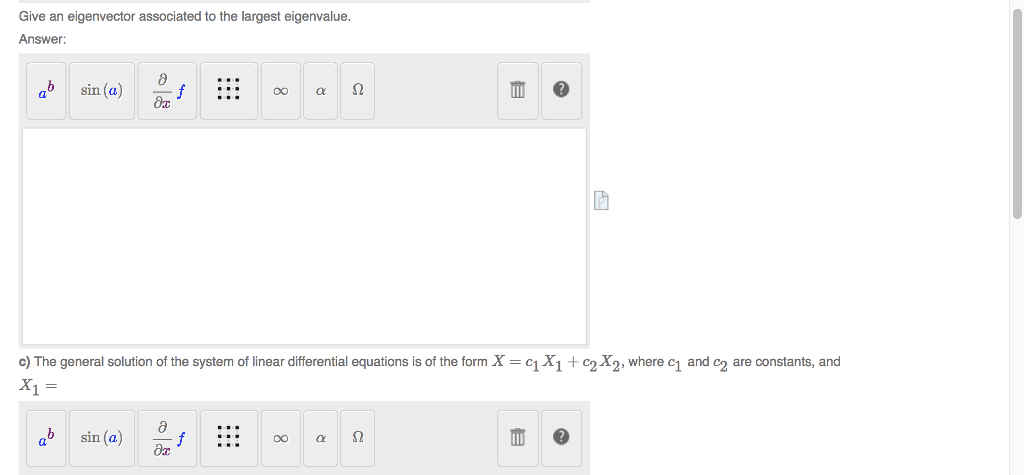
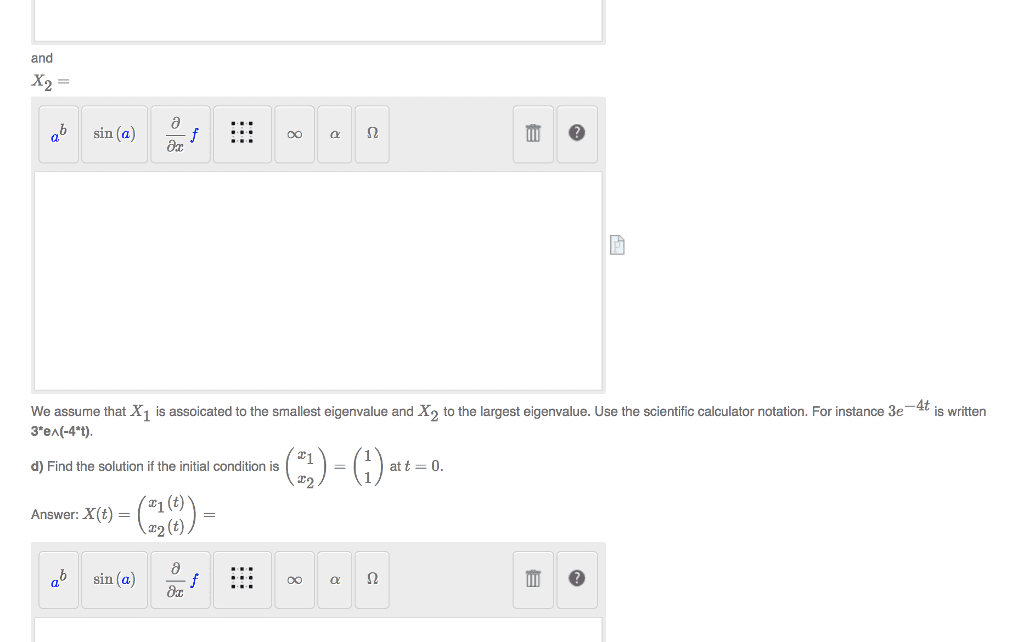
MATH 121A Final: SampleFinal-121A

66 views2 pages

turquoisegnu128

31 Jan 2019

School

Department

Course

Professor

For unlimited access to Study Guides, a Grade+ subscription is required.

Document Summary

Math 121a winter 2017 (the emphasis for these sample questions is on the earlier material. For more practice with eigenvectors and eigenvalues, see this week"s homework and this week"s se 101 worksheet. R3 given by (x, y) 7! (x, 0, x): r2, p (r) ! P (r) given by f (x) 7! xf (x): r3. 1 + 2x + 3y + 4z: let t : v ! V be the linear transformation t : (a1, a2, a3, . 7! (0, a1, a2, : let ei denote the sequence with 1 in position i and with 0 everywhere else. Why is {e1, e2, . not a basis for v ? (hint. Reread the de nition of linear combination from section 1. 4. : prove that this linear transformation has no eigenvectors, why doesn"t this contradict our theorem that every linear transformation on a nite-dimensional.

Related Questions

Show transcribed image text

harlequinserval672

Q1. Write the expression 6/(2 + 8i) in the standard form a + bi.
a. -1/5 + 4i/5
b. 3/17 + 12i/17
c. -1/5 - 4i/5
d. 3/17 - 12i/17

Q2. Choose the graph of the number line that represents x â¤ -3.
a.
b.
c.
d.

Q3. Write the expression â-64 and express your answer in the standard form a + bi.
a. iâ8
b. 8i
c. -8i
d. Â±8

Q4. Evaluate (2xy + 35)/x given that x = 5 and y = 7.
a. 7
b. 49
c. 9
d. 21

Q5. The net income y (in millions of dollars) of Pet Products Unlimited from 1997 to 1999 is given by the equation y = 9x2 + 15x + 52, where x represents the number of years after 1997. Assume this trend continues and predict the year in which Pet Products Unlimited's net income will be $598 million.
a. 2005
b. 2004
c. 2003
d. 2006

Q6. Solve the equation x2 + 144 = 0 in the complex number system.
a. {-12, 12}
b. {12}
c. {12i}
d. {-12i, 12i}

Q7. Find the real solutions of the equation â24x + 48 = x + 8.
a. {-4}
b. {6}
c. {-3}
d. {4}

Q8. Solve P-5Q/3=(P+7)/2+1 for P.
a. P = (15 - 10Q)/3
b. P = (27 + 10Q)/3
c. P = (27 - 10Q)/3
d. P = (15 + 10Q)/3

Q9. Tracy can wallpaper 2 rooms in a new house in 8 hours. Together with her trainee they can wallpaper the 2 rooms in 6 hours. How long would it take the trainee working by herself to do the job?
a. 8 hr
b. 30 hr
c. 22 hr
d. 44 hr

Q10. Solve x2 - 2x - 24 = 0 by using completing the square.
a. {â5, -1}
b. {-6, 4}
c. {-20, -4}
d. {6, -4}

burgundypug228

Answer 1-44 with steps and explanations.

MATH 121A Final: SampleFinal-121A

Document Summary

Get access

Related textbook solutions

Calculus

Single Variable Calculus: Early Transcendentals

CALCULUS:EARLY TRANSCENDENTALS

Related Documents

MATH 121A Midterm: SampleMidterm1

MATH 121A Midterm: SampleMidterm2-121A

MATH 405 Study Guide - Midterm Guide: Irreducible Polynomial, Unit Circle, Solution Set

Related Questions