MATH 126 Midterm: MATH 126 UW Midterm 1 Spring 13perkinsExIans

• School: UW
• Department: Mathematics
• Course: MATH 126
• Professor: All

Document Summary

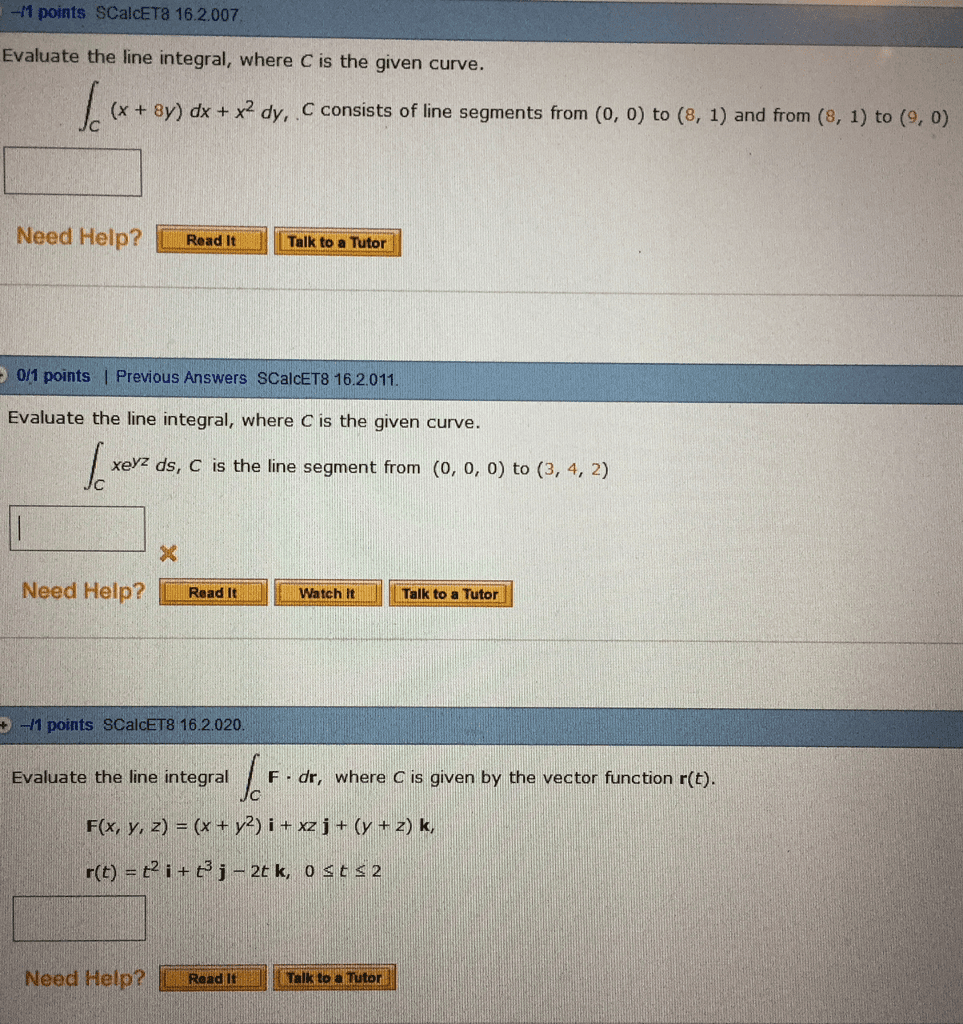
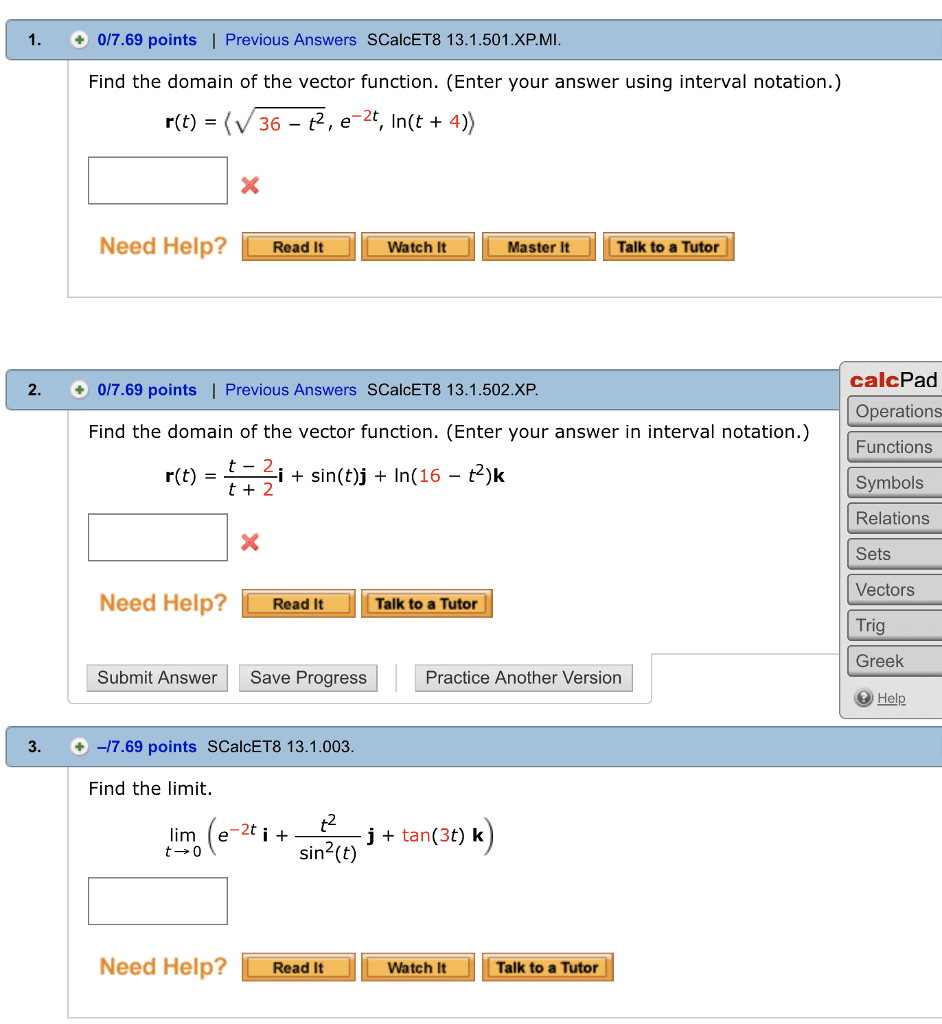
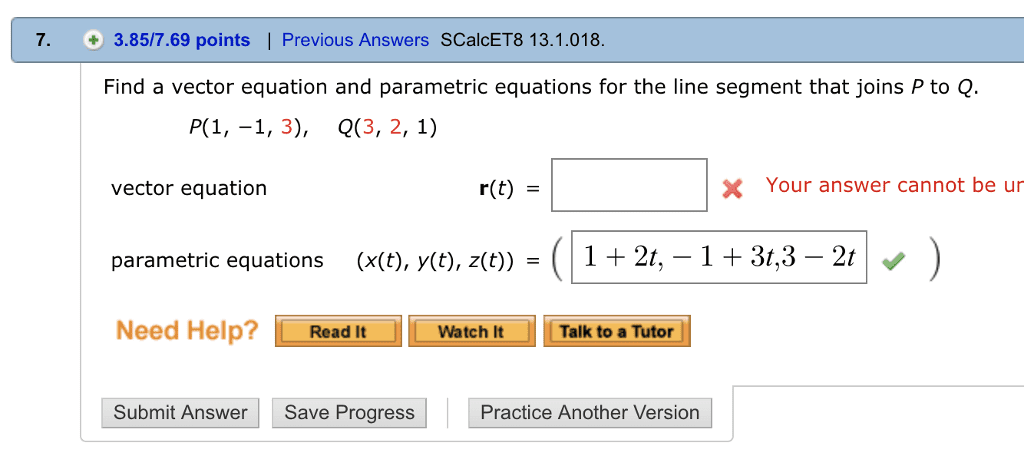
0 r(t) dt = 3 tan 1 t i + ln(cid:16)1 + t2(cid:17) j(cid:12)(cid:12)(cid:12)(cid:12) Consider the curve in r2 with parametric equations x = 4t2+t+1, y = t4+2t. Give the coordinates of the points on the curve where the tangent line has slope 2. dy dt. We need to solve dx dt dy dx. 4t3 + 2 = 2 (8t + 1) 4t3 16t = 0 t = 0, 2, 2 t = 0 gives the point (1, 0). t = 2 gives the point (19, 20) t = 2 gives the point (15, 12) Consider the curves r1(t) = ht + 1, t2 + 3, 3t + 1i and r2(s) = hs + 4, s2, 2si. (a) (5 points) Solve the linear system t + 1 = s + 4. 3t + 1 = 2s t = 1, s = 2. to get.