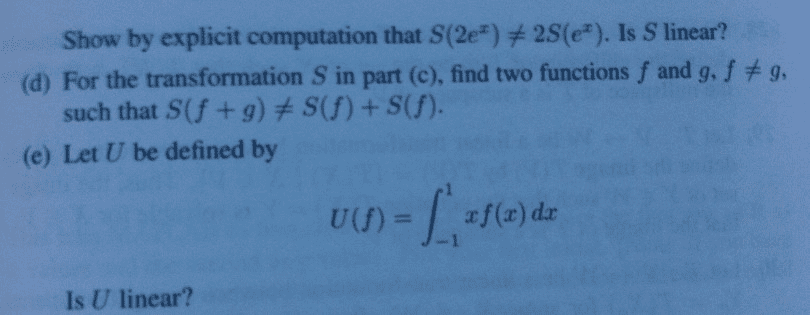MATH 405 Study Guide - Midterm Guide: Linear Map

39 views1 pages

turquoisegnu128

10 Jan 2019

School

University of Maryland

Department

Mathematics

Course

MATH 405

Professor

All

For unlimited access to Study Guides, a Grade+ subscription is required.

Document Summary

You may assume that dim v = 2. Show that the image of t cannot be the subspace of f 7 determined by the equation x1+x2+x3+x4+x5+x6+x7 = 0: (30 points) let p3(f ) denote the polynomials of degree 3 with coe cients in f and let. M2(f ) denote the 2 2 matrices with coe cients in f . T : p3(f ) m2(f ) by. T (f ) = " f (1) f (1) f (1) # . f (1) (you may assume that t is linear. ) (a) with respect to the standard bases of these vector spaces compute the matrix of. , vk are a basis for w . , fn be the dual basis of v de ned by v1, . Finally, de ne w 0 = {f v |f (w) = 0 w w }. You may assume that w 0 is a subspace of v .

Related Questions

Let P denote the vector space of all polynomials and f'(x)denote the derivative of all numbers in P. State true or false tothe following:

1. T: R^2 --> R^3 defined by T(x,y)=(?^2x,0, y/2) is a linear transformation

2. T: R^2 --> R^3 defined by T(x,y)=(x+y, x-y, xy) is alinear transformation

3. T: R^2 --> R^3 defined by T(x,y)=(1,0,0) is a lineartransformation

4. T: R^2 --> R^3 defined by T(x,y)= (y, x, y) is a lineartransformation

5. T: R^2 --> R^3 defined by T(x,y)= (x, x^2, x^3) is alinear transformation

6. T: R^2 --> R^3 defined by T(x,y)= (2x+3y, 3x+4y, 4x+5y) isa linear transformation

7. T: P --> P defined by T(f(x))= f(0) +f'(0)x + f''(0)x^2 isa linear transformation

8. T: P --> P defined by T(f(x))= f(1) + f'(2) + f''(3)x^2 isa linear transformation

9. T: P --> P defined by T(f(x))= f(x-3) is alinear transformation

10. T: P --> P defined by T(f(x))= f(x)-3 is a lineartransformation

tantoad80

Let P f '(x ) denote the derivative of f in P .

Let Pk denote the vector space of all polynomials with degreeless
than or equal to k. Define a linear transformation T : P4 --> P3by
T (f(x)) = f(0) + f '(1)(x - 1) + f ''(2)(x - 2)^2 + f '''(3)(x -3)^3 .
Find the matrix representation for T relative to the standardbasis
{1, x, x^2 , x^3 , x^4 } of R4 and the reversed standard basis {x^3, x^2 , x, 1}
of R3 .

yellowpanda130

linear algebra

MATH 405 Study Guide - Midterm Guide: Linear Map

Document Summary

Get access

Related textbook solutions

Calculus

Single Variable Calculus: Early Transcendentals

CALCULUS:EARLY TRANSCENDENTALS

Related Documents

MATH 405 Study Guide - Midterm Guide: Linear Map

MATH 405 Study Guide - Final Guide: Jordan Normal Form, Hermitian Adjoint, Linear Map

MATH 405 Midterm: MATH405_BOYLE-M_SPRING2011_0101_MID_EXAM_1

Related Questions