MATH 152 Midterm: MATH 152 TAMU 2015a X3H Solutions
Document Summary
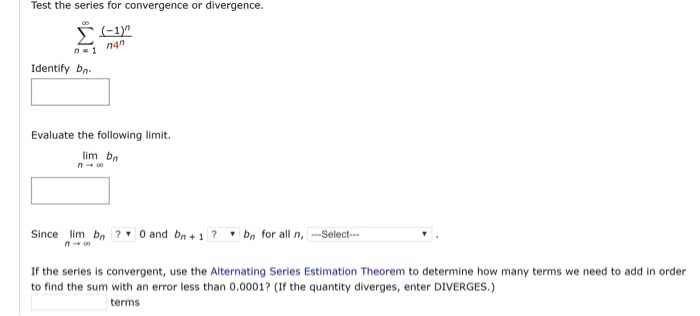
Thu, 30/apr c(cid:13)2015 art belmonte: approximate the sum of the series correct to four decimal places. Cite relevant test(s). n=1 ( 1)n 1 n 4n: this series converges by the alternating series. Test (ast) since bn = |an| = 1 n 4n 0: for a partial sum of the series to be accurate to 4 decimal places, we need the remainder to satisfy. Estimation theorem (aset), (n+1)4n+1 5 10 5 for n 5. 1: therefore s5 = 5 n=1 ( 1)n 1 n 4n 0. 2231, determine whether the series n=2 ( 1)n n ln n is absolutely convergent, conditionally convergent, or divergent. Cite relevant test(s): the series converges by the alternating series. Test (ast) since bn = |an| = 1: however, |an| diverges by the integral test: R x ln x dx = limb (ln (ln b) ln (ln 2)) = . ( 1)n: hence n ln n is conditionally convergent. n ln n 0. n=2.