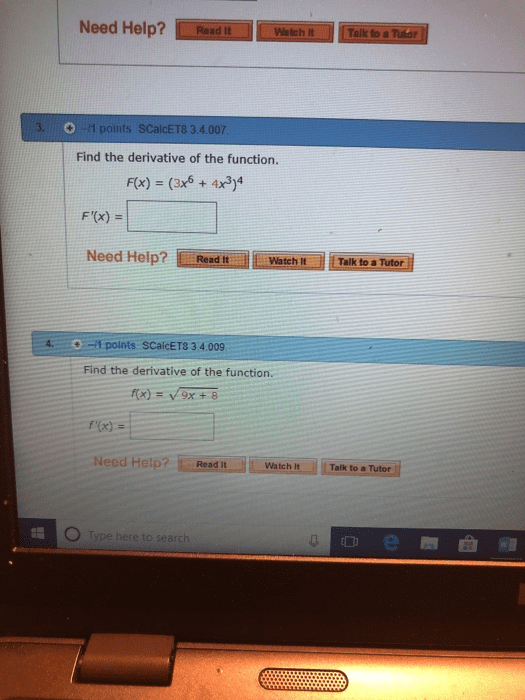
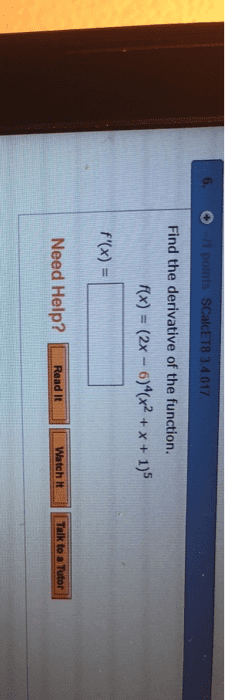
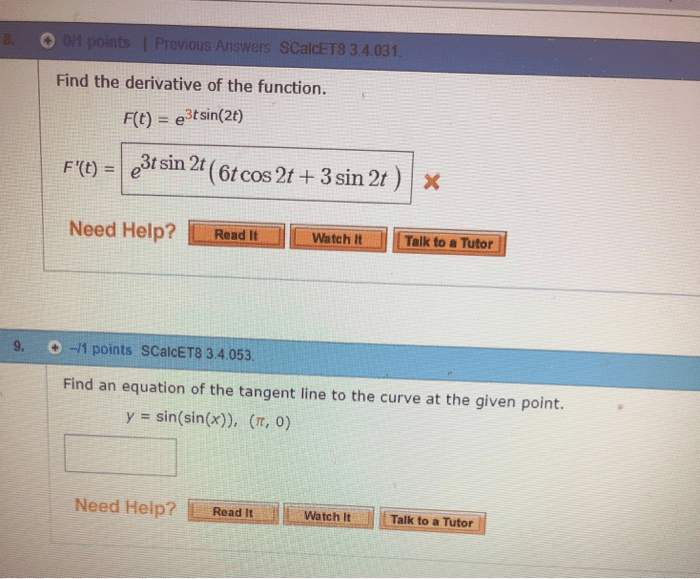
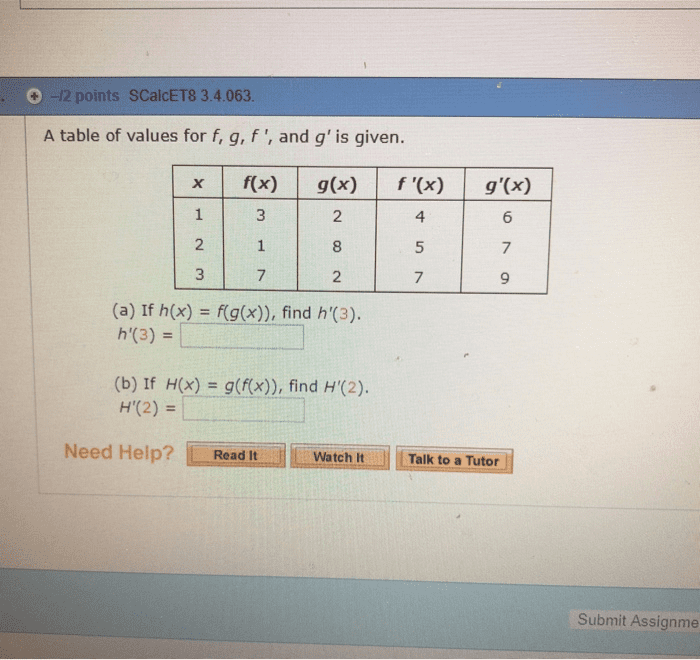
MAT 122 Quiz: MAT 122 SBU Quiz 7 Solution

• School: Stony Brook University
• Department: Mathematics
• Course: MAT 122
• Professor: All

Document Summary

Question 1: consider the function h(x) = (x2 4)2. (a) find the rst derivative h (x) using the chain rule. The inside function is g(x) = x2 4 and the outside function is f (z) = z2. We have that g (x) = 2x and f (z) = 2z. Therefore the derivative is h (x) = f (g(x)) g (x) = 4x(x2 4) (b) find the critical points of h(x). The critical points are where h (x) = 0. We need to check the sign of the derivative on the intervals ( , 2), ( 2, 0), (0, 2), and (2, ). Using a number line to display our answer gives. To nd in ection points, we rst need to nd the second derivative. = 4x3 16x h (x) = 12x2 16 (we could also have used the product rule to take the derivative).