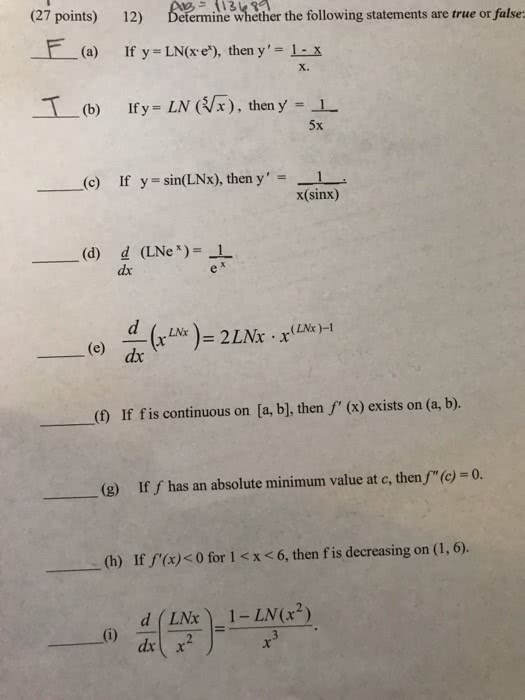MTH 421 Midterm: Midterm 1 Spring 2009 Solutions

27 views7 pages

turquoisegnu128

31 Jan 2019

School

Department

Course

Professor

For unlimited access to Study Guides, a Grade+ subscription is required.

Document Summary

February 18, 2009: determine whether each of the following statements is true or false. If a statement is false, provide a counterexample. (write out the word true or false completely!) (a) let f , g : [a, b] r be integrable functions. Assume that f (x) g(x) for all x [a, b], a g(x) dx. and that there exists a point c [a, b] so that f (c) > g(c). Thenr b a f (x) dx >r b. Let [a, b] = [ 1, 1], let g(x) = 0, and let f (x) =(1. Then f (x) g(x) for all x [ 1, 1], f (0) > g(0), but r 1. 1 f (x) dx = r 1 (b) let f : (a, b) r be a locally integrable function. Then |f | is a locally integrable function. If f is locally integrable, then by de nition f is integrable on any interval.

Related Questions

5. (18 pts) Circle True if the statement is ALWAYS true; circle False otherwise. No explanations are required. Let f be a one-to-one function and f its inverse. (a) If the point (2, 5) lies on the graph off, then the point (5,2) lies on the graph of f. True False f (2) = 5 f-1 (5) = 2 (b) sin-1 (T) = 0 True False Since >1, ris not in the domain of sin-?; | or sin-1 (7) #0, since sin (0) = 0 # Iff and g are two functions defined on (-1, 1), and if (c) limg (x) = 0, then it must be true that lim[ f(x) g (x)] = 0. True False Let f (x) = 1 / x, if x #0, and f (0) = 4 and g(x) = x. Then lim g (x) = lim (x) = 0, but Lim ( f (x) g(x)] = lim [() x] = 18 0. Iffis continuous on (-1, 1), and if f (0) = 10 and lim g (x) = 2, (a) True False then lin (= 5. Because lim : (*) - Limx-of (*) .f(0) = 20 = 5 If f is continuous on [1, 3], and if f(1) = 0 and f(3) = 4, then the equation f(x) = (e) has a solution in (1, 3). True False Since f continuous on [1, 3), f(1) = 0 < < 4 = f (3), by the Intermidiate Value Theorem there exists a cin (1, 3) such that f (c) = . (f) Let f be a positive function with vertical asymptote x = 5. Then lim f (x) = +0. True False Let f (x) = 1, if x < 5, and f (x) ==, ifx>5. Then lim f (x) = +00, and therefore, X = 5 is a vertical asymptote. 5 - X So, f is a positive function with vertical asymptote x = 5 but lim f (x) + +co, since lim f (x) = + 0 + lim f (x) = 1, which means that lim f (x) does not exist.

[8] 9. Either prove the statement is true or show that it is false. (a) sin (sin(2)) = 27. Solution: It is FALSE. The range of sin-' r is (-1,1], hence sin (sin(27)) = sin (0) = 0 (b) If f is continuous at a, then f is continuous at a. Solution: It is TRUE. Let g(x) = \f()]. If lim f(x) = f(a), then we have since the absolute value function is continuous lim g(x) = lim f() = lim f(x) = f(a) = g(a) So, g = \f is continuous at a. (c) If [g] is continuous at a, then g is continuous at a. -1 if r <0 Solution: It is FALSE. Let g(x) = 3 · Then, g = 1, so g is continuous at 0 i if >0 by the Continuity Theorems, but lim g(t) = -1 + lim g(1) 240- 1- 0+ So, g(x) is not continuous at a. (d) If f is continuous at a, then f is differentiable at a. Solution: It is FALSE. We know that f(1) = 2 is continuous at 0, but is not differentiable at 0.

MTH 421 Midterm: Midterm 1 Spring 2009 Solutions

Document Summary

Get access

Related Documents

MTH 421 Midterm: Midterm 2 Spring 2009 Solutions

MTH 421 Midterm: Midterm 2 2017

MTH 421 Midterm: Midterm 2 Spring 2009

Related Questions