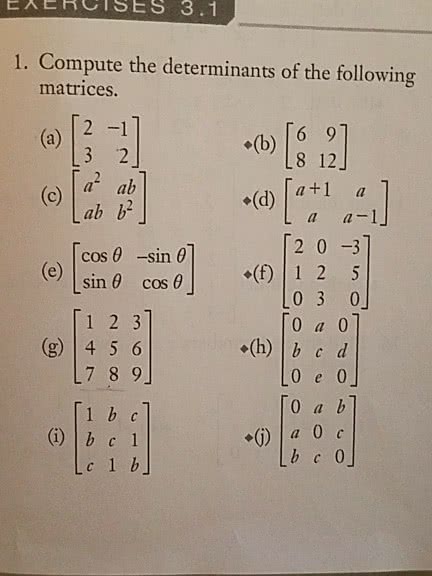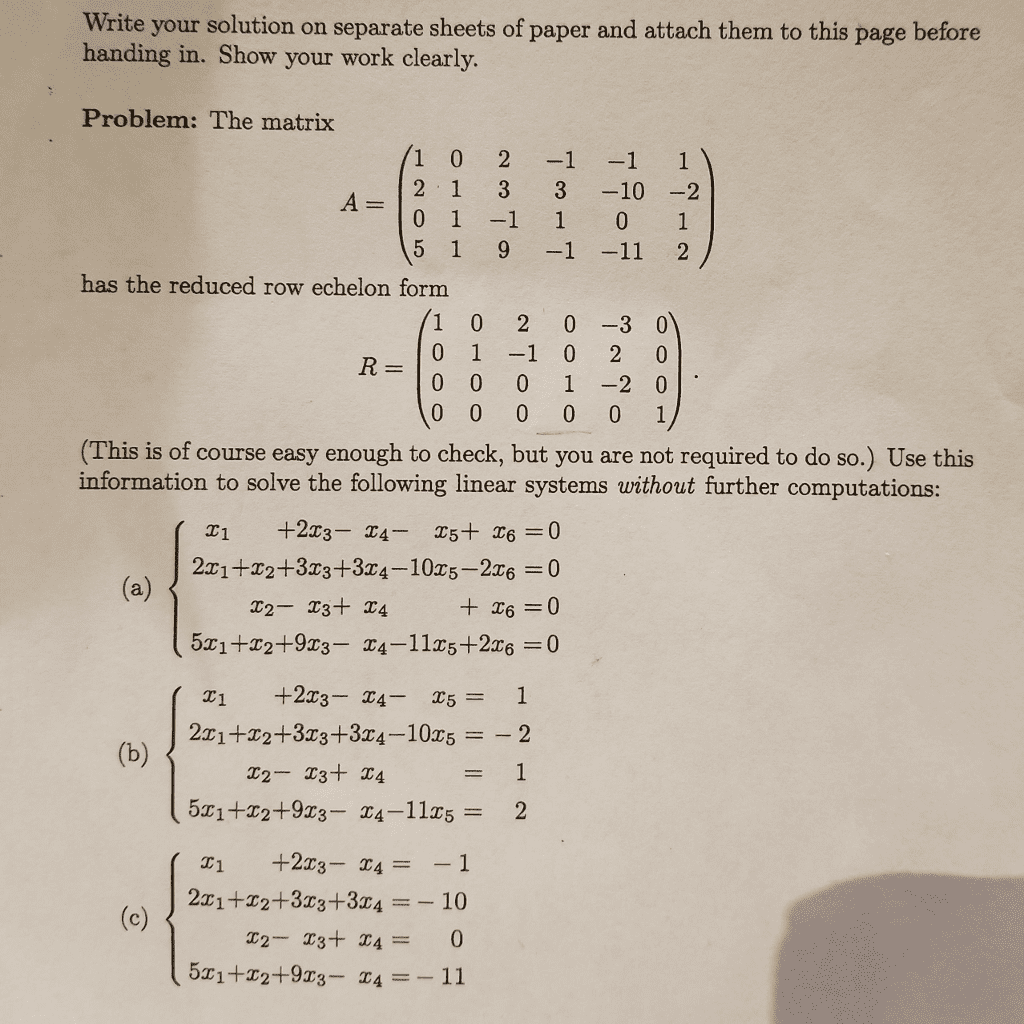MATH 551 Final: MATH 551 KSU Final Practice 1 s16

• School: Kansas State University
• Department: Mathematics
• Course: MATH 551
• Professor: All

Document Summary

Show all of your work clearly and in order to receive credit. Problem 2 (a) find the inverse of a. 1 (b) use a 1 from part (a) to solve the following linear system x1 + x2 x3 = 1. 2x1 + x2 + x3 = 0 x1 x2 + x3 = 2. Problem 3 assume x, y, z are real numbers. (a) find all orthogonal matrices of the form. 0 z (b) find the determinant for each of the orthogonal matrices found in part (a). X1 + 2x2 x3 4x4 = 0. Problem 5 (a) find an orthonormal basis for the subspace u = span{u1, u2, u3} where u1 = 1 (b) find the projection of v = [1 0 1 2]t onto u . Problem 6 find the dimension and a basis for the column space, row space and null space of the given matrix a. Problem 7 compute the eigenvalues and eigenvectors of the matrix.