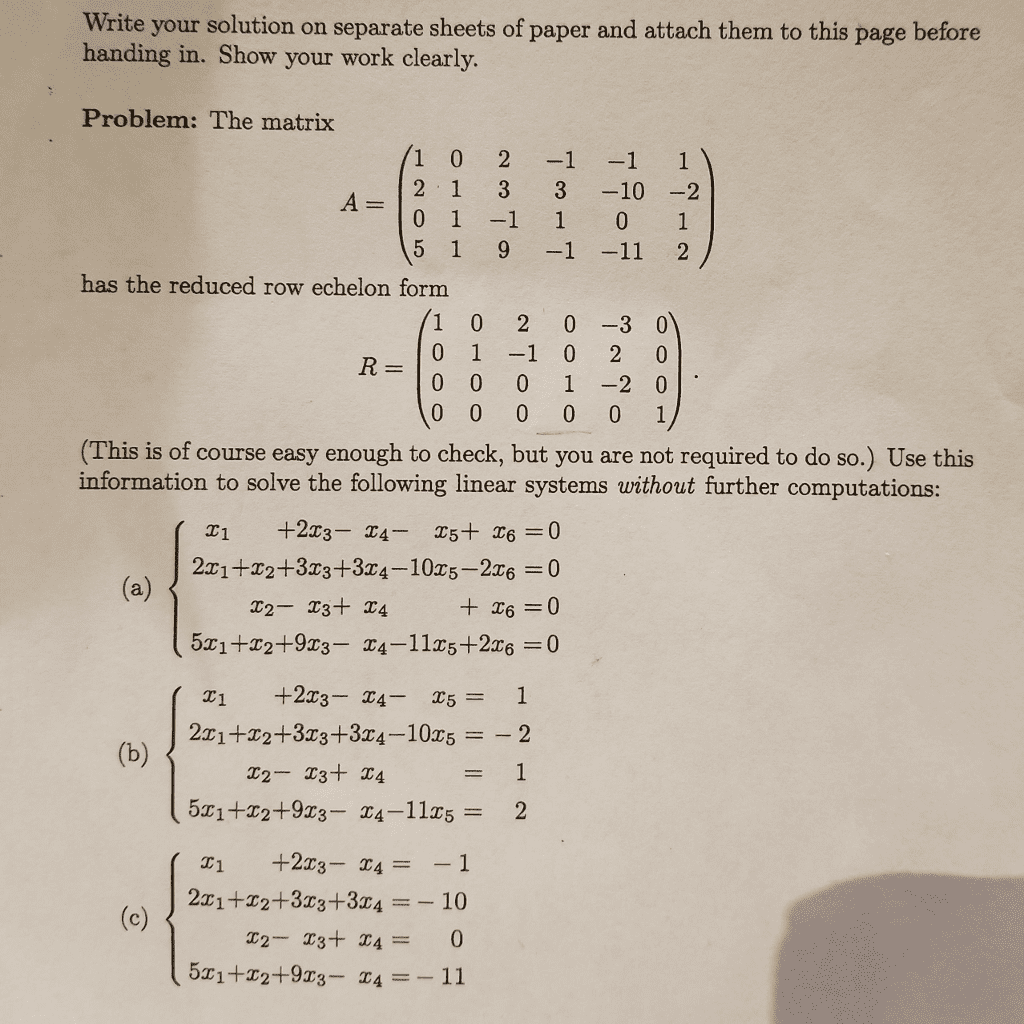MATH 551 Final: MATH 551 KSU Final Practice f17

• School: Kansas State University
• Department: Mathematics
• Course: MATH 551
• Professor: All

Document Summary

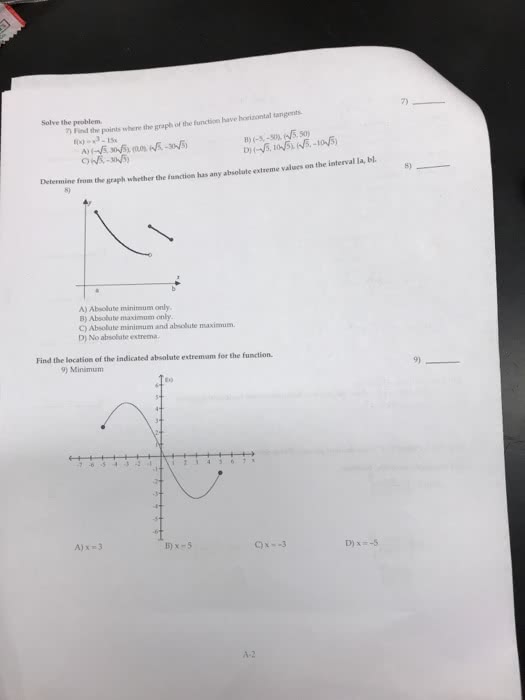
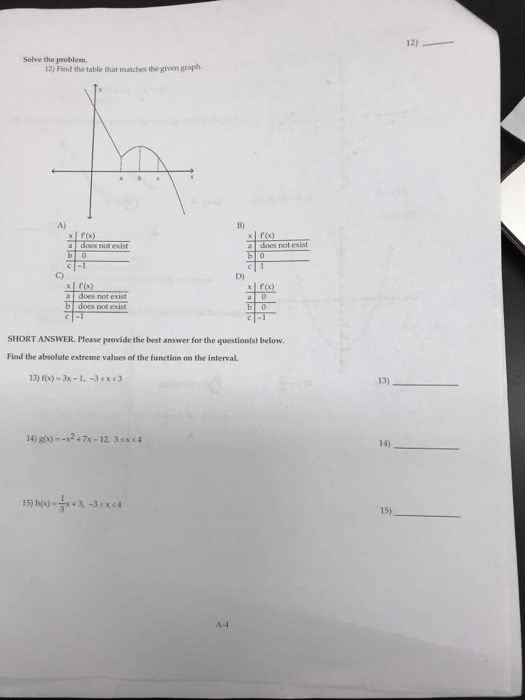
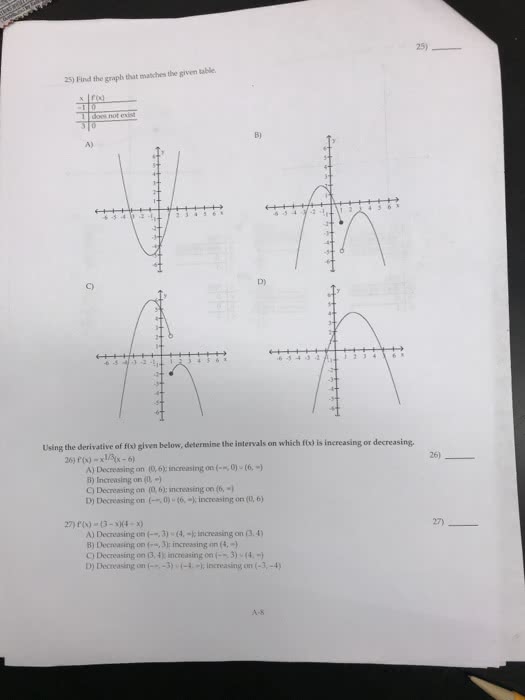
You must show your work clearly and in order to receive credit. Problem 1 [10 points] determine if matrices a and b are row-equivalent. Problem 2 [10 points] find an lu factorization of the matrix and check your result by multiplication: Problem 3 [10 points] write b has a linear combination of v1 and v2 or show that it"s impossible. Problem 4 [10 points] consider the subspace s = span{v1, v2, v3, v4} of r3 where v1 = . Find a subset of the vi"s that forms a basis of s. show how the redundant vi"s are expressed in terms of the basis and compute the dimension of s. Problem 5 [10 points] show that the set of all vectors x = [x1 x2 x3 x4]t in r4 that satisfy the equations below is a subspace of r4. Find a basis for it. (cid:26) x1 + 3x2 + x3 + 2x4 = 0.