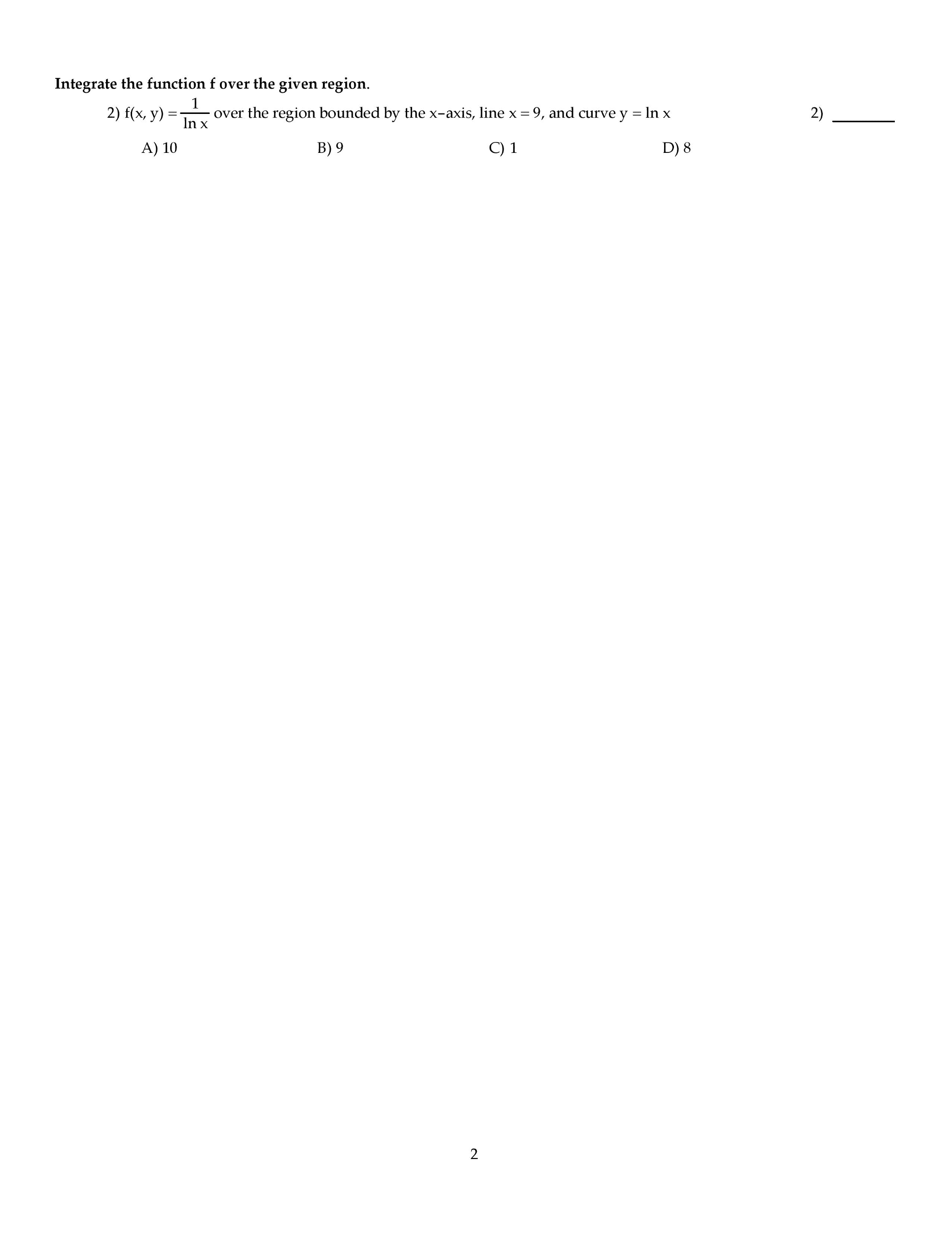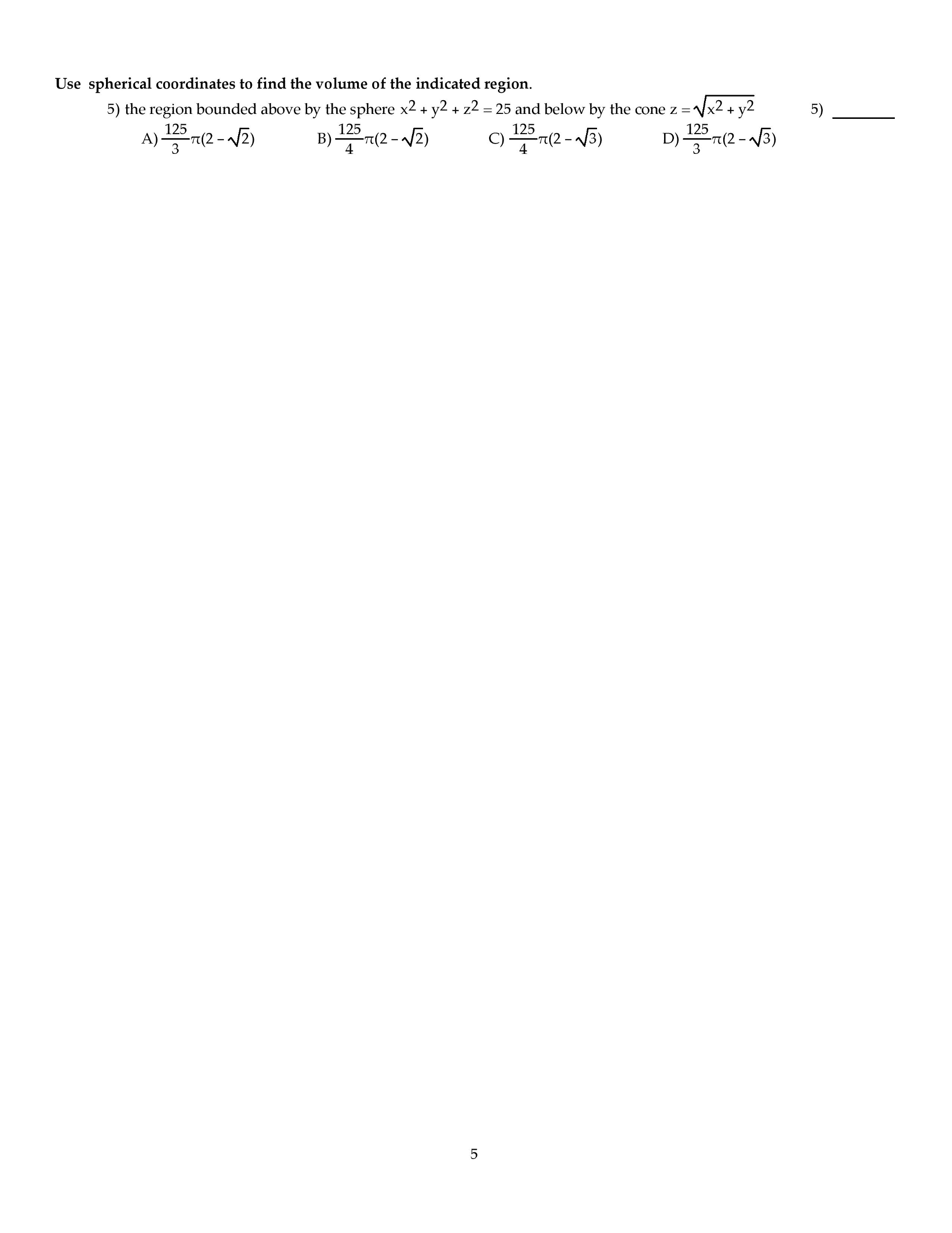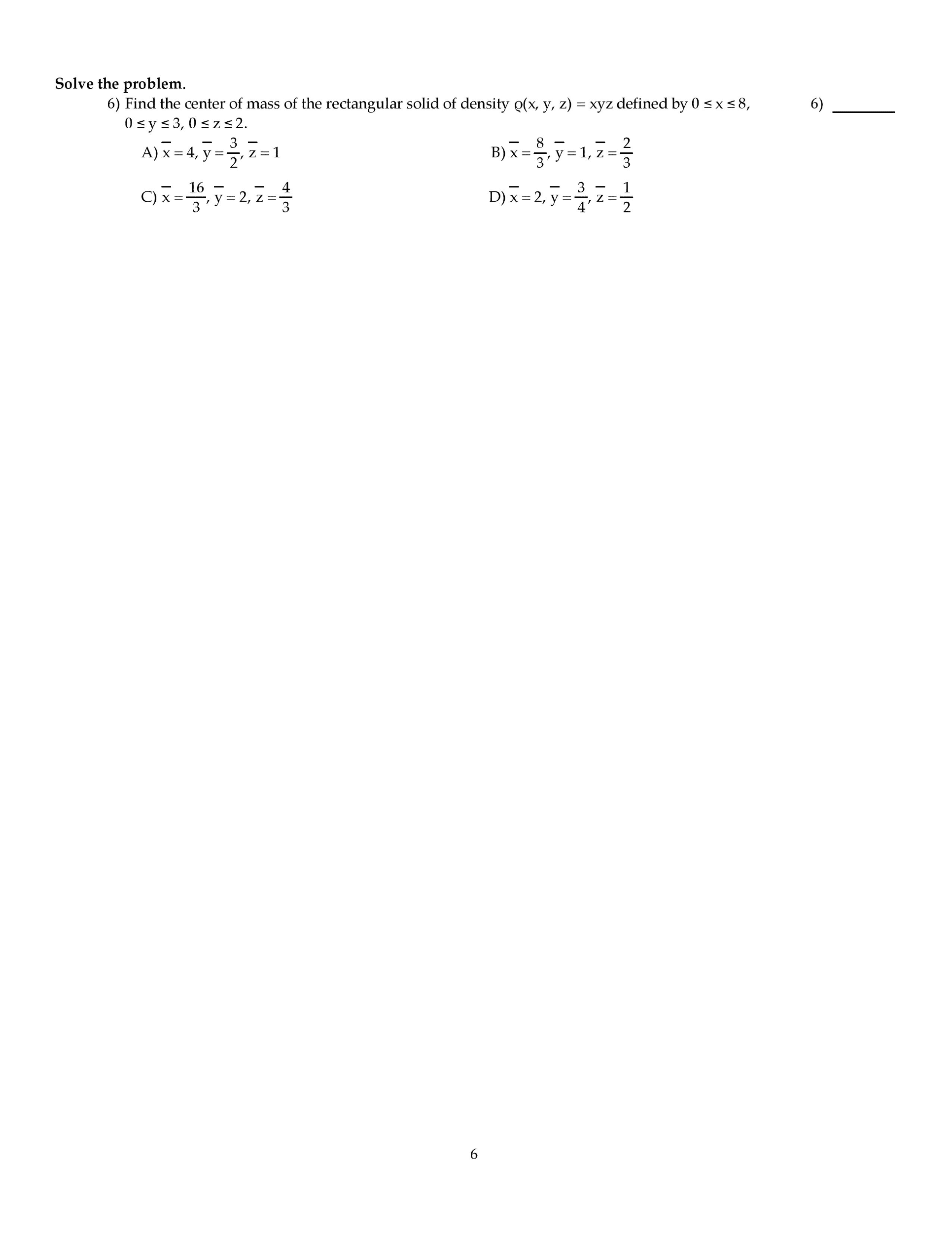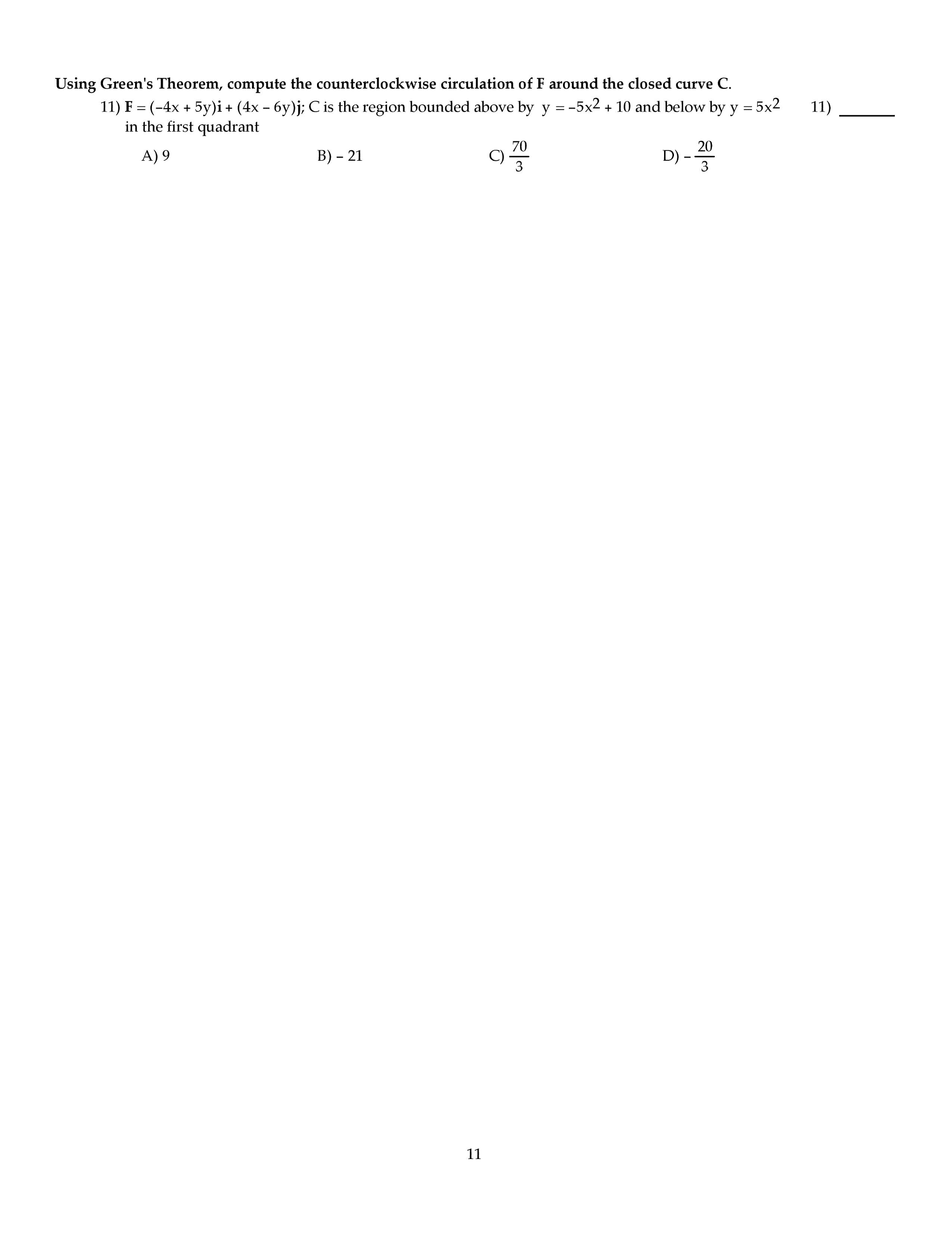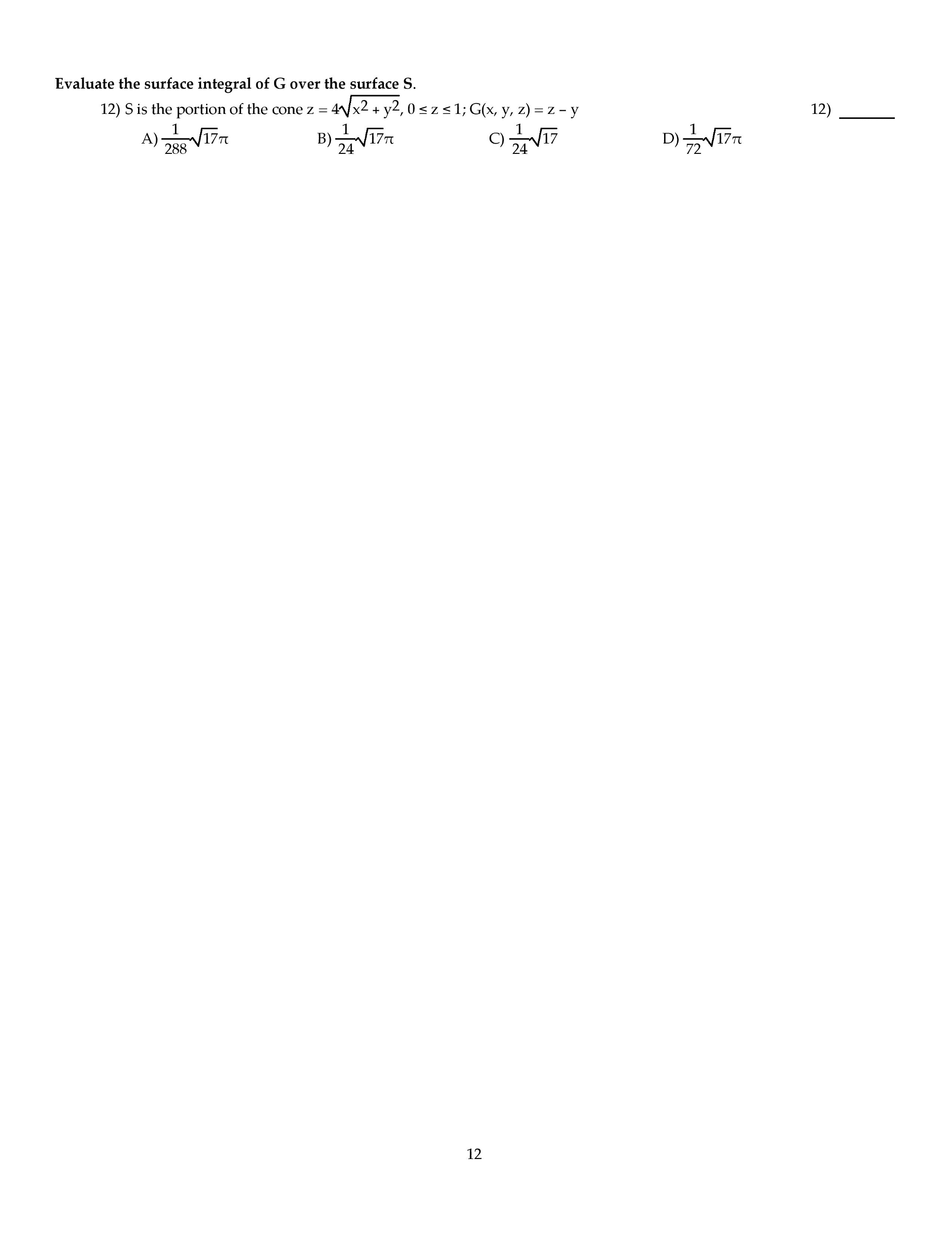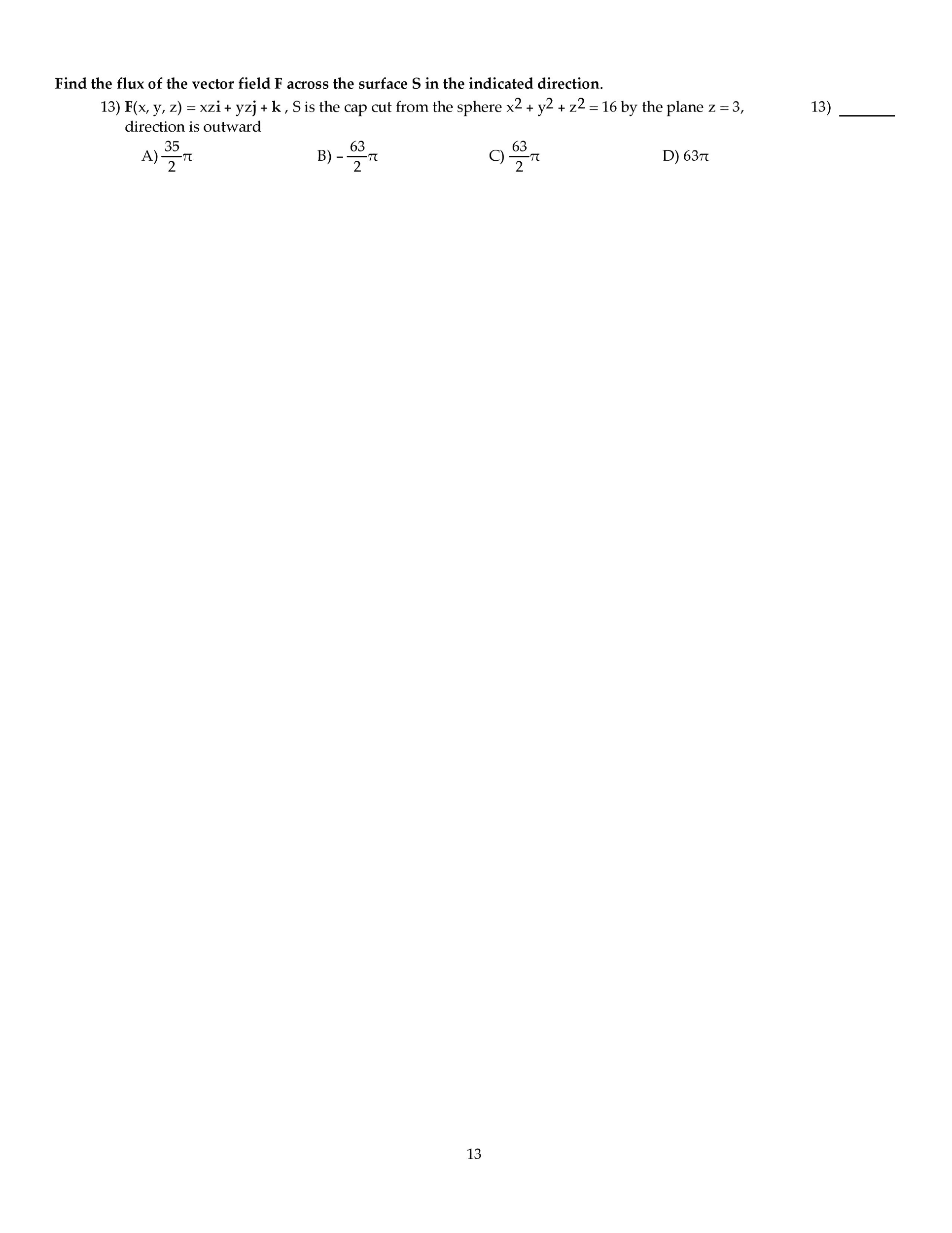MATH 551 Midterm: MATH 551 KSU Test 2s06 a
15 Feb 2019
School
Department
Course
Professor
Document Summary
Use the back page as a sketch paper. For full credit, show your work in detail. We have shown that the functions {1, x, x2, x3} are linearly independent. Find the matrix m representing d with respect to the basis {1, x, x2, x3}. Where a, b, c are real numbers. (i). Show that the inverse (i a) 1 = i + a + a2. An economy system consists of three sectors e, f and g. the consumption matrix c is given by page 2. If the external demand is d = [50, 60, 70]t, nd the production vector x = [l, m, n]t. For the following ordered basis b = {x1 = [1, 3, 2]t, x2 = [ 1, 1, 1]t, , x3 = [5, 1, 4]t} in r3. (a). Find the point transform matrix pb and coordinate transform matrix cb (b). Let x = [21, 21, 21] r3, nd its b-coordinate.
