MATH 551 Midterm: MATH 551 KSU Test1 S15
15 Feb 2019
School
Department
Course
Professor
Document Summary
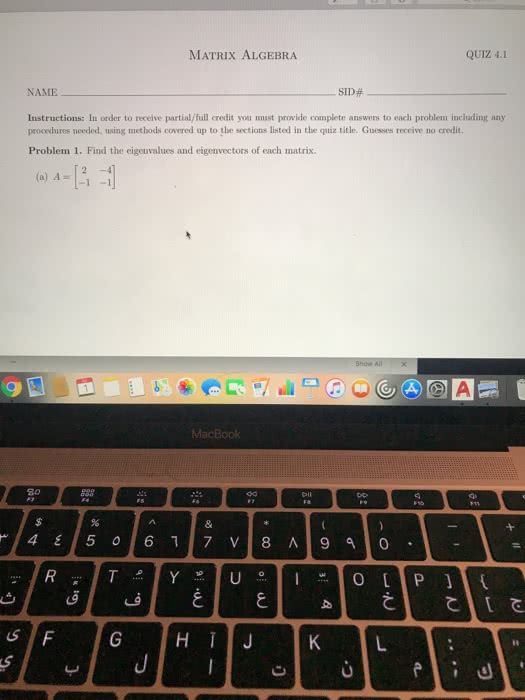
You must show your work clearly and in order to receive credit. Problem 1 [10 points] find all the eigenvalues and eigenvectors for the matrix. Problem 2 [10 points] use the rref algorithm to nd the inverse of the matrix a and check that your result is correct: Problem 3 [10 points] determine whether the following matrices are equivalent by nding a reduced row echelon form. Problem 4 [10 points] draw the graph whose adjacency matrix is a. Also compute the cubic power of a and nd all walks with 3 hops from node 1 to node 4. Problem 5 [10 points] use the adjacency matrix of problem 4 to compute the laplacian matrix. 1a current entering in node 2 and exiting in node 4. Then write down an incidence matrix by orienting the edges somehow and compute the current. And what are the dimensions of c? (b) suppose x is an 6 1 vector.
