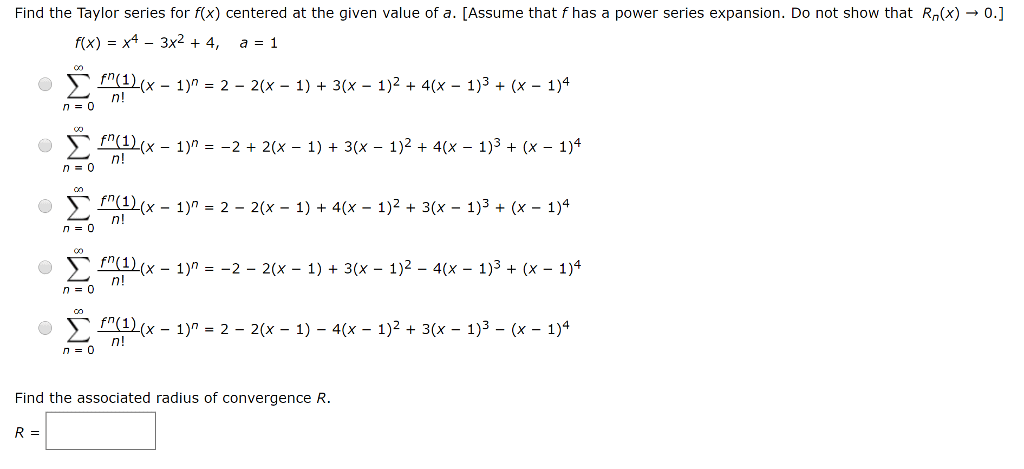MATH 166 Final: MATH 166 Final Exam 2 Spring 2017
Document Summary
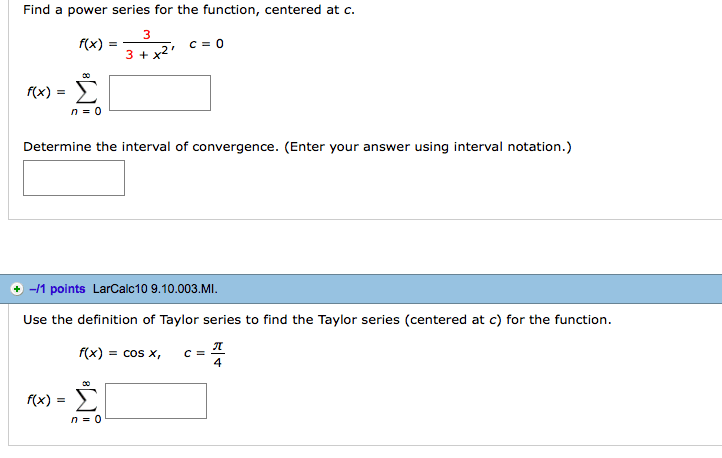
Find the exact value of xn=0: find the exact value of xn=0, find the exact value of xn=1. 1 n2n : determine if the following series converges conditionally, converges absolutely, or diverges: Xn=1 cos( n) ln(n) n: determine if the following series converges conditionally, converges absolutely, or diverges: Xn=1 n3n (3n): determine the interval of convergence for the following power series: xn=1 (x 2)2n n4n, determine the interval of convergence for the following power series: xn=10, (a) show that (1 + x) 1/2 = xn=0. )2 (b) find the taylor series for arcsin(x). (hint: dx(cid:0) arcsin(x)(cid:1) = 1 d. |f(3)(y)| 6 m for all y between 0 and 2. M |x a|n+1 (c) recall (cid:12) (cid:12)f(x) pn(x)(cid:12) (cid:12) 6 (n + 1)! where. Pn(x) is the taylor polynomial of order n centered at a and |f(n+1)(y)| 6 m for all y between a and x.