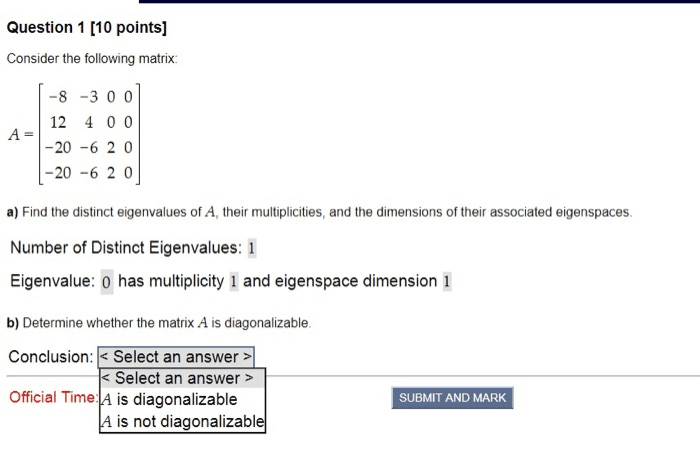
MATH 1502 Study Guide - Quiz Guide: Diagonalizable Matrix, Invertible Matrix
Document Summary
Find the eigenvalues and corresponding eigenvectors to the matrix (cid:18) 1. A = (cid:18) 1 (cid:19: find a15 (show all work), solve xn = a xn 1, x(0) , suppose b is a 4 4 matrix with three distinct eigenvalues. One eigenvalue has geometric multiplicity one and one has geometric multiplicity two. 2: let l be the line in r3 given by. 1 and y = [2, 1, 1]t: find the orthogonal projection of y onto l, find the matrix representing the orthogonal projection onto l, find the matrix that represents the re ection of a vector about l. Two matrices a and b are similar if b = p 1ap where p is an invertible matrix. Show that a and b have the same determinant. Show that a and b have the same characteristic polynomial. 4(a) let a be an m n matrix.