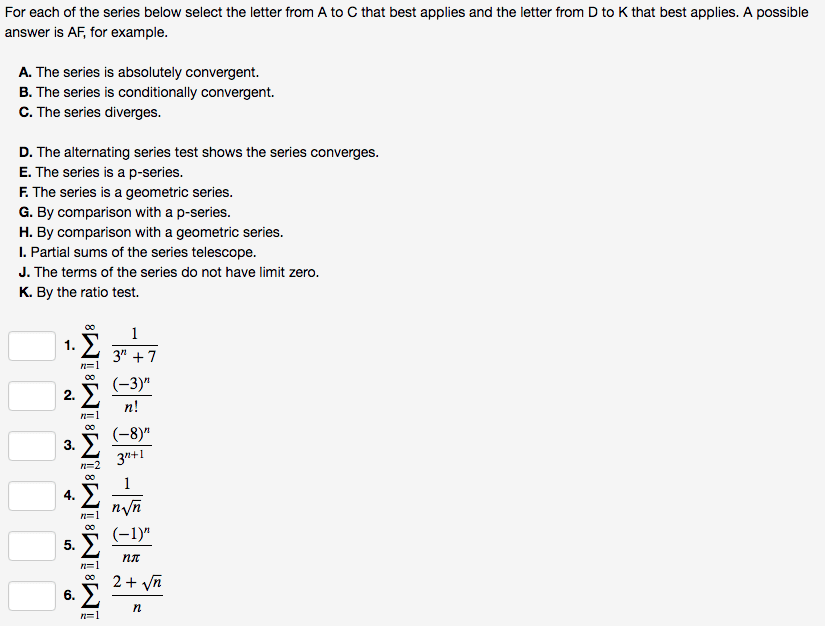APPM 1360 Midterm: appm1360fall2014exam3_sol

APPM 1360 Exam 3 Solutions Fall 2014
1. (8 points each) Determine whether the series is absolutely convergent, conditionally convergent, or
divergent.
(a)
∞
X
n=2
(−1)n
ln n(b)
∞
X
n=1
(−1)n+1 n2
(n+ 1)2(c)
∞
X
n=1
sin 2n−1
2π
n
Solution:
(a) The series converges by the Alternating Series Test: bn+1 =1
ln(n+ 1) <1
ln n=bnand
lim
n→∞
1
ln n= 0. The series is not absolutely convergent because
∞
X
n=2
1
ln ndiverges by the Direct
Comparison Test. Compare to the divergent harmonic series
∞
X
n=2
1
n. Since 1
ln n>1
n, the series
∞
X
n=2
1
ln nalso diverges. Therefore the given series is conditionally convergent .
(b) The series is divergent by the Test for Divergence: lim
n→∞
n2
(n+ 1)2= 1 ⇒lim
n→∞
(−1)n+1n2
(n+ 1)2
does not exist since the sequence alternates between values close to 1and −1for large n.
(c) The series equals 1−1
2+1
3−1
4+··· =
∞
X
n=1
(−1)n−1
nwhich is the convergent alternating
harmonic series. The series is not absolutely convergent because the harmonic series
∞
X
n=1
1
n
diverges. Therefore the given series is conditionally convergent .
2. Consider the series
∞
X
n=0
(−1)n+1(x−1)n+1
n+ 1 .
(a) (7 points) Find the radius of convergence.
(b) (9 points) Find the interval of convergence.
Solution:
(a) Use the Ratio Test.
lim
n→∞
an+1
an
= lim
n→∞
(x−1)n+2
n+ 2 ·n+ 1
(x−1)n+1
= lim
n→∞
(x−1) ·n+ 1
n+ 2
=|x−1|
The series is absolutely convergent when |x−1|< R =1.
Document Summary
Fall 2014: (8 points each) determine whether the series is absolutely convergent, conditionally convergent, or divergent. (a) 2 (cid:1) n (a) the series converges by the alternating series test: bn+1 = lim n . Xn=1 ( 1)n 1 n which is the convergent alternating harmonic series. The series is not absolutely convergent because the harmonic series diverges. Therefore the given series is conditionally convergent : consider the series. Xn=0 ( 1)n+1(x 1)n+1 n + 1 (a) (7 points) find the radius of convergence. (b) (9 points) find the interval of convergence. Solution: (a) use the ratio test. lim n (cid:12)(cid:12)(cid:12)(cid:12) an+1 an (cid:12)(cid:12)(cid:12)(cid:12) = lim n (cid:12)(cid:12)(cid:12)(cid:12) (x 1)n+2 n + 2 n + 1 (x 1)n+1(cid:12)(cid:12)(cid:12)(cid:12) = lim n (cid:12)(cid:12)(cid:12)(cid:12) (x 1) n + 1 n + 2(cid:12)(cid:12)(cid:12)(cid:12) The series is absolutely convergent when |x 1| < r = 1 .