MAT-2130 Midterm: MATH 2130 App State Fall2011 Test3

14 views4 pages

turquoisegnu128

15 Feb 2019

School

Department

Course

Professor

For unlimited access to Study Guides, a Grade+ subscription is required.

Document Summary

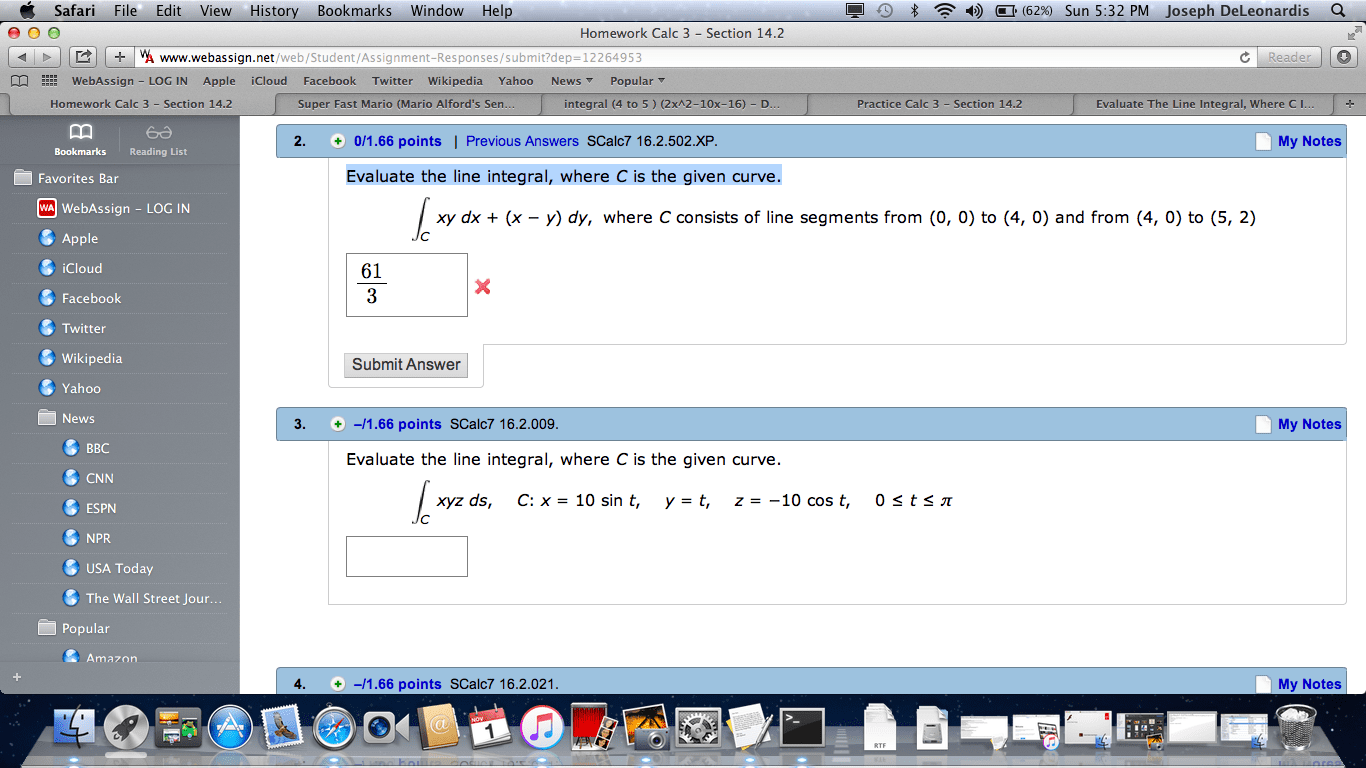
Be sure to show your work! x = cos( ) sin( ) y = sin( ) sin( ) z = 2 (1 + cos(2 ): (15 points) consider z 2. Sketch the region of integration and then evaluate the integral. Hint: r ey2 dy is impossible to evaluate. Reading o the bounds on the iterated integral, the region of integration is bounded by y = x/2, y = 1, x = 0, and x = 2. Since the antiderivative of ey2 is not something we are familiar with, we need to reverse the order of integration to nd the answer. Notice that (as a type ii) region the bounds are: 0 x 2y and 0 y 1. Z 2 x/2 ey2 dy dx = z 1. Change coordinates using u = 3x y and v = x + y. R da where r is bounded by y = 3x + 1, y = 3x + 2, y = x, and.

Related Questions

Change the order of integration and evaluate the triple integral... integral^(pi)_0 integral^(pi)_0 integral^5sin(phi)_0 (rho)^2*sin(phi)d(rho)d(theta)d(phi) please show all work and be sure to change the order of integration... Question #6

1. (45 marks) Short-Answer Questions. Put your answer in the box provided but show your work also. Each question is worth 3 marks, but not all questions are of equal difficulty. Full marks will be given for correct answers placed in the box, but at most 1 mark will be given for incorrect answer. Unless otherwise stated, it is not necessary to simplify your answers in this question. a) Find the equation of the tangent plane to the graph of the function z = f(x,y) = sell at (0,1). Answer b) Evaluate (T, 0) if f(x,y) = sin(ry). Answer c) Graph of a function z = f(x,y) is given by: Which of the following level curves correspondes to this function. Answer d) If f(x,y) = e(3x – 2y), find lim - Math)-f(x,y) e) Find % if f(x, y) = x2 - y3 and 2 = r sin(t), y = r cos(t). Answer f) Evaluate the directional derivative of f(x, y) = !at (1, -1) in the direction of u =(2, 1). Answer 8) Does Simono converge? h) Sketch the direction field of the differential equation = 1-2y. i) Consider the differential equation ay = 15 - 31, y(0) = 0, and use Euler's method with step size 0.1 to estimate y(0.1). Answer j) Knowing that (-3,-3) is a critical point of f(x,y) = 2:3 + y2 – 4.cy -3.0, use the second derivative test to find out whether it is a local minimum, local maximum, or a saddle point. Answer k) Solve the initial value problem, dy dt 642 2y + cos(u) y(1) = . Answer 1) Is ū=(2,2, -1) perpendicular to v = (5,-4, 2)? Answer m) Find the area between the graph of y = 1 + sin(x) and y=1-sin(x) from 0 to 7. Answer n) Determine the lentgh of the curve y = 8/2,0 SIS 3. Evaluate and simplify your answer. Answer o) Express the volume of the solid obtained by rotating the bounded region that lies between curves y = (x-2)2 and y=1,150 $4 about the vertical line 2 = 5. Do not evaluate this integral. Answer

Evaluate the line integral, where C is the given curve #2

MAT-2130 Midterm: MATH 2130 App State Fall2011 Test3

Document Summary

Get access

Related Documents

MAT-2130 Midterm: MATH 2130 App State Spring2013 Test1 answer key

MAT-2130 Midterm: MATH 2130 App State Fall2005 Exam1 answer key

MAT-2130 Midterm: MATH 2130 App State Spring2012 Test3

Related Questions