MATH128 Quiz: MATH 128 Spring 2013 Assignment 10a.pdf
Document Summary
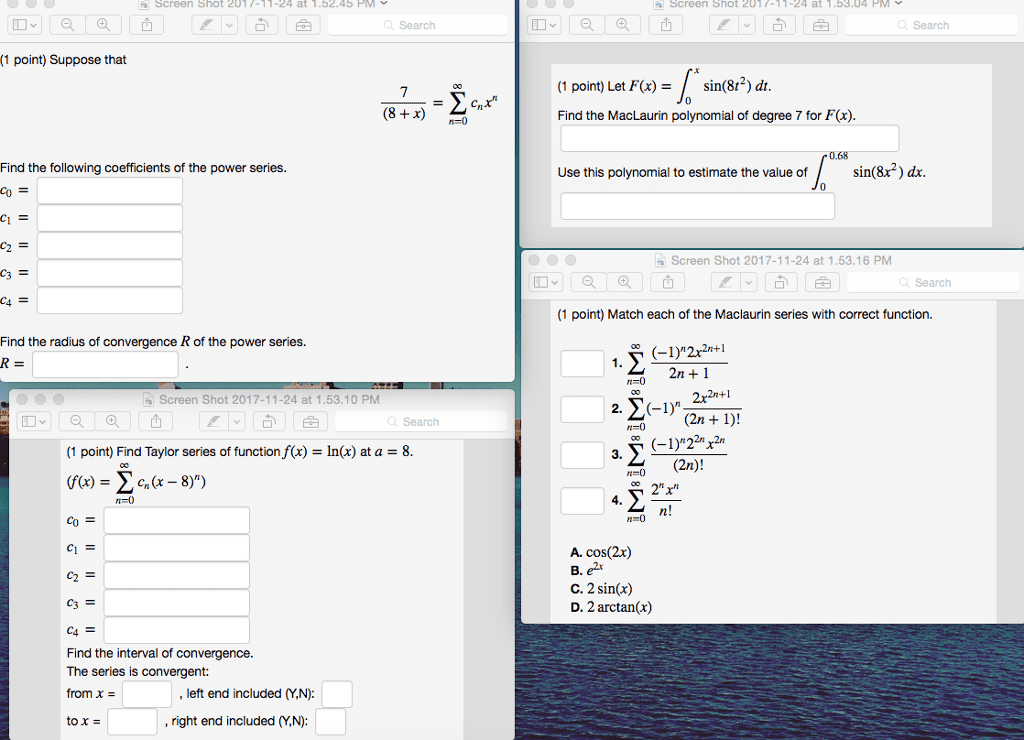
This is less than 1 ax n n. F(2k)( /2) = 0, f(4k+1)( /2) = 1, f(4k+3)( /2) = 1. We can ignore the even terms because they are zero, so we have . )2/ for all x, so the radius of convergence is : f(x) = ln x at a = 3 f (x) = 1/x, f (x) = 1/x2, f (x) = 2/x3, f(4)(x) = (3! )/ x4, f(n)(x) = ( 1)n 1 (n 1)!/xn f(3) = ln 3, f (3) = 1/3 = 0, f (3) = 1/32 = 1/9, f (2) = 2/27, f(4)(3) = 6/81 = 2/27, f(n)(3) 2 n n n n n n n n n n. 3 when |x 3| < 3; radius of convergence is 3: f(x) = x sin 2x at a = 0. The taylor series for sin x at a = 0 is n. , so the series for sin 2x is.