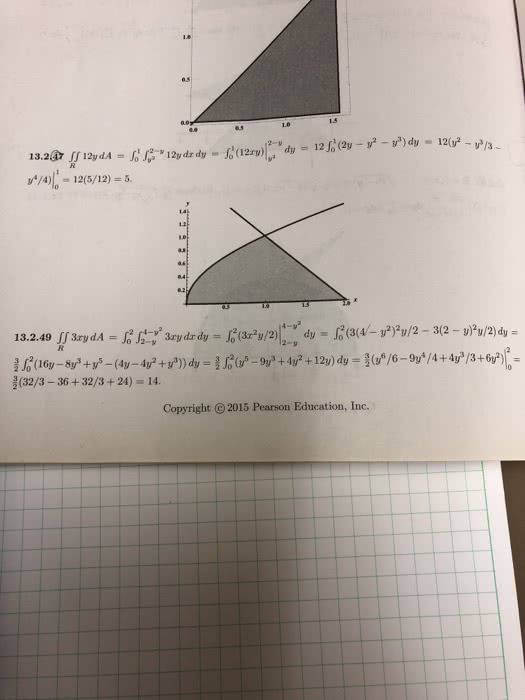
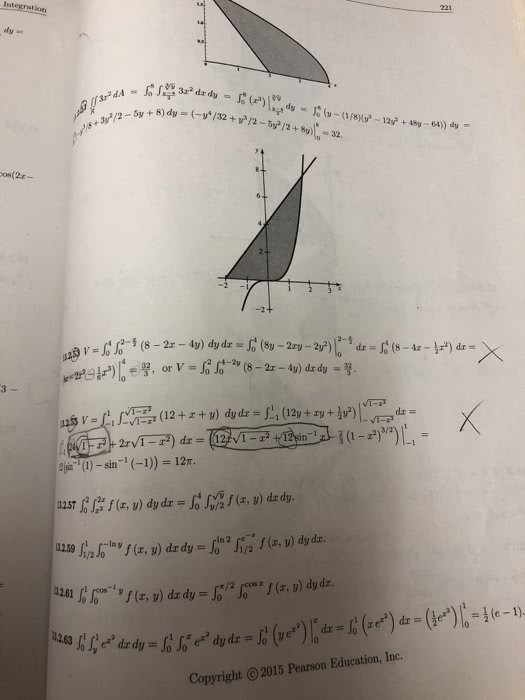MATH 264 Study Guide - Final Guide: Multiple Integral, Surface Integral, 2 On

• School: McGill University
• Department: Mathematics and Statistics
• Course: MATH 264
• Professor: Sancho

Document Summary

Solutions (1) with the aid of a change of variables, compute the value of the integral. Zz(d) 1 y2 da region (d) in the rst quadrant of the x, y plane bounded by the curves x2 + y2 = 1, x2 + y2 = 4, x = 2y, x = 4y. Solutions: let x = r cos , y = r sin . Then, where 2 = arctan(1/2), 1 = arctan(1/4). (d) : r = 1 2; = 1 2, y2 da = zz(d) . 1 r2 sin2 rdrd = ln r . 1 (2) find the area of that portion of the surface z2 = x2 + y2 above the rst quadrant of the (x, y)-plane for which x 1 and y 2. Solutions: the projection of (s) on xy plane is (a) : (0 x 1; 0 y 2). Area = zz(s) ds = zz(a)q1 + z2 x + z2 ydxdy = zz(a)