MATH 4B Lecture 4: MATH 4B
MATH 4B verified notes
4/10View all
Document Summary
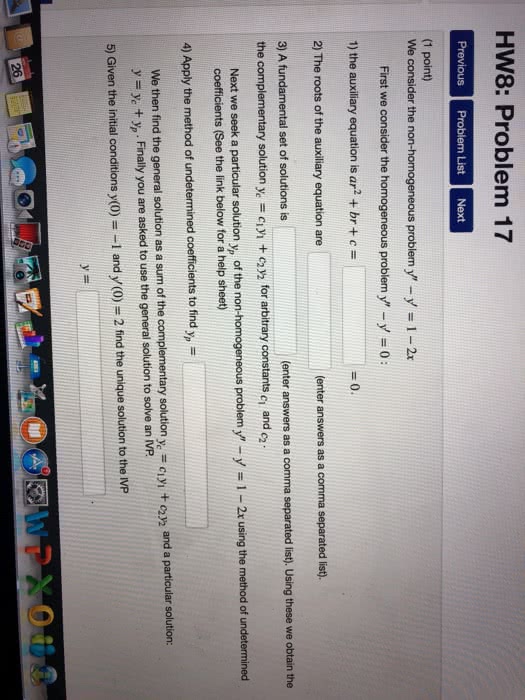
Homogenous second order linear differential equations. c allowing won - constant coefficients) Ett y - is some solution to this equation . y = ett. Cd "s d - 3) as an operator span felt , e- tf c y = c , e. A vector associated to t : v v where. It v is a space of differential functions , operator . e. g . Test =3 eh and t is a differential est is an eigenfunction of the derivative. For more complicated operator . say y. Factor cd - 3) cd - i ) and apply to y ( d - 3) cdy ty 7=0. 39=0 ( dti ) c dy - 397=0 solutions in span felt , etf. The functions e t and e- are eigenfunctions of cd "s d - 3) with eigenvalue o. Order of futons doesn"t matter ( dtl ) i d - 3) e- t.