HomeClass Notes1,200,000CA670,000

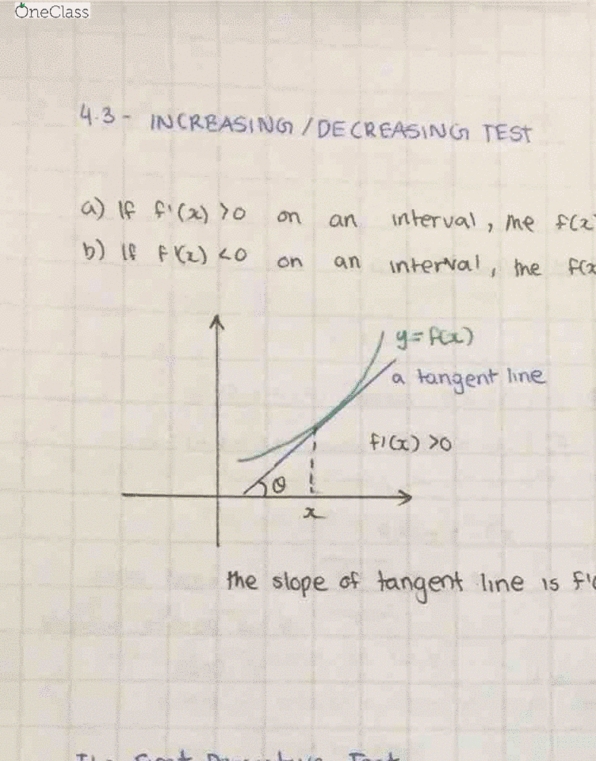
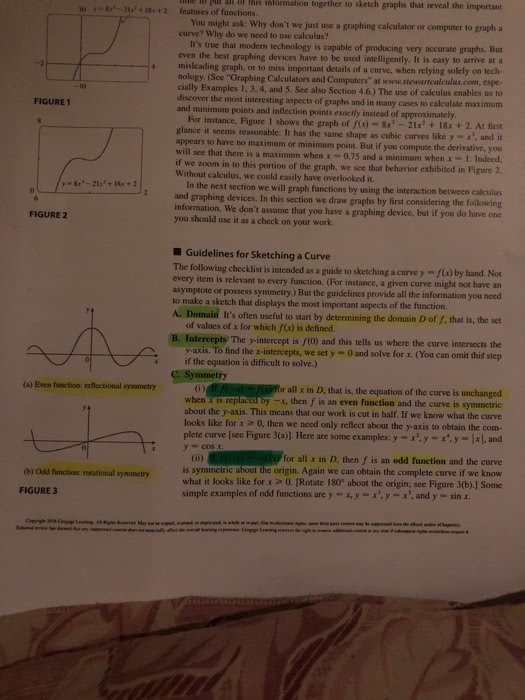
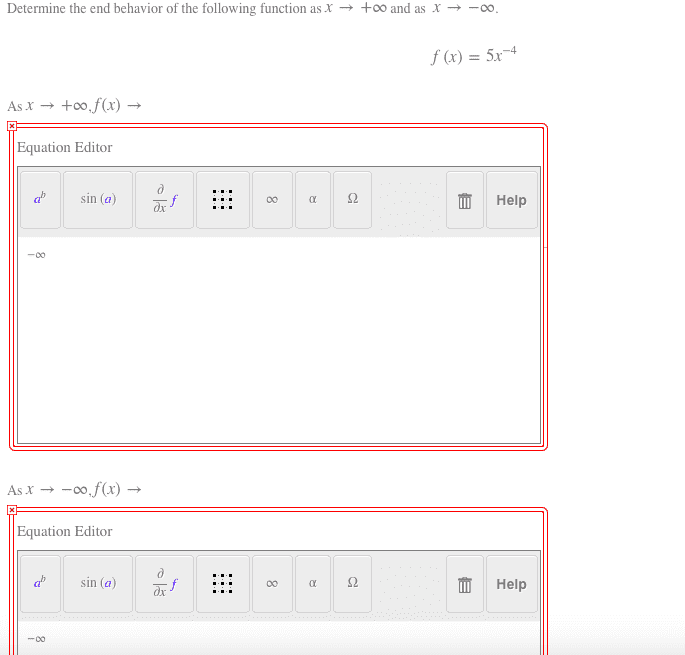
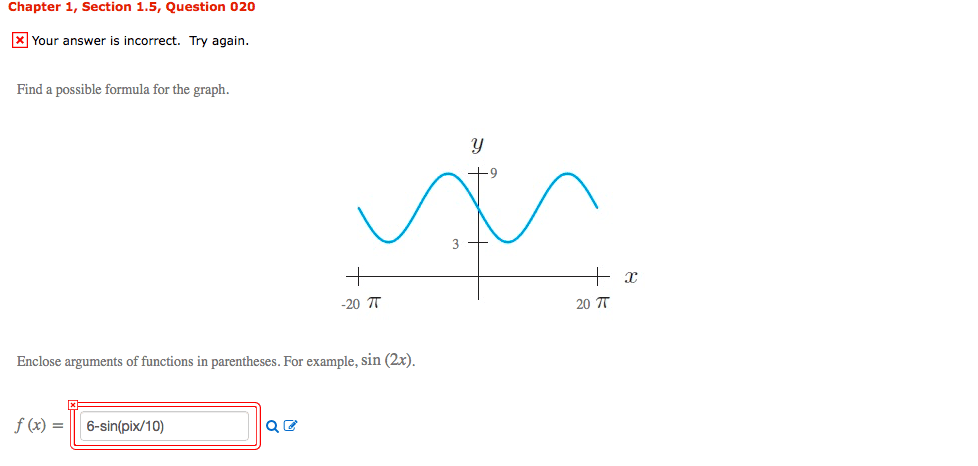
Calculus 1000A/B Lecture Notes - Lecture 34: Mean Value Theorem, Antiderivative

25 views2 pages

Verified Note

12 Nov 2018

School

Western University

Department

Course

Calculus 1000A/B

Professor

For unlimited access to Class Notes, a Class+ subscription is required.

CALC 1000A/B verified notes

Calculus 1000A/B Lecture Notes - Lecture 33: Hne, Mox Fuel

Calculus 1000A/B Lecture Notes - Lecture 34: Mean Value Theorem, Antiderivative

Calculus 1000A/B Lecture Notes - Lecture 35: Summation, Antiderivative

Document Summary

Calculus 1000a lecture 34 section 4. 9 antiderivatives. Midterm marks have been sent out- check owl or school email; quiz 3 available for pickup. We can start by introducing the definition of antiderivatives: A function f is called an antiderivative of f on an interval i if f(cid:859)(cid:894)x(cid:895)= f(cid:894)x(cid:895) for all (cid:858)x(cid:859) in the interval i. Let"s look at a simple example: based on this definition, we know that we will be looking for a power function of order three. Example 1: (cid:1858)(cid:4666)(cid:4667)=(cid:2870) find the antiderivative f check that f(cid:859)(cid:894)x(cid:895)= x2= f(x: recall = (cid:2869, (cid:4666)(cid:3119)(cid:4667) =(cid:885)(cid:2870) (cid:4672)(cid:3119)(cid:2871)(cid:4673)=(cid:2869)(cid:2871)(cid:885)(cid:2870)=(cid:2870, therefore, we could say that the antiderivative is (cid:4666)(cid:4667)=(cid:3119)(cid:2871) For example, we could write (cid:4666)(cid:4667)=(cid:3119)(cid:2871)+(cid:1855), as we know that the derivative of a constant is zero. We have found an antiderivative, but how would we know if there are other antiderivatives that satisfy have various theorems to help us answer this question: now, we need to get the coefficient to be 1.

Related Documents

Calculus 1000A/B Lecture Notes - Lecture 35: Summation, Antiderivative

Calculus 1000A/B Lecture Notes - Lecture 42: Antiderivative

Calculus 1000A/B Lecture 41: Calculus 1000 A -Lecture 41- Section 5.3- The Fundamental Theorem of Calculus

Related Questions

Sketch using these guidelines

pul aill al thes information together to sketch graphs that reveal the important You might ask: Why don't we just use a graphing calculator or computer to graph a It's true that modern technology is capable of producing very accurate graphs. But K 21+1+2 features of functions curve? Why do we need to use calculus? even the best graphing devices have to be used intelligently. It is easy to arrive at a misleading graph, or to miss important details of a curve, when relying solely on tech- nology. (See "Graphing Calculators and Computers" at www.stewartcalcelus.com, espe 4 discover the most interesting aspects of graphs and in many cases to and minimum points and inflection points exocily instead of approximately cially Examples 1, 3.4, and 5. See also Section 4.6.) The use of calculus enables us to calculate maximum FIGURE 1 For instance, Figure I shows the gr aph of /(x)-è¨-21x, + 18x + 2.At first glance it seems reasonable: It has the same shape as cubic curves like y x and it appears to have no maximum or minimum point. But if you compute the derivative, you will see that there is a maximum when x-0.75 and a minimum when x 1. Indeed if we zoom in to this portion of the graph, we see that behavior exhibited in Pigure 2 Without calculus, we could easily have overlooked it. 6a, FIGURE 2 In the next section we will graph functions by using the interaction between calculus and graphing devices. In this section we draw graphs by first considering the foilowing information. We don't assume that you have a graphing device, but if you do have one you should use it as a check on your work. â Guidelines for Sketching a Curve every item is relevant to every function. (For instance, a to make a sketch that displays the most important aspects of the function. The following checklist is intended as a guide to sketching a curve y- f(x) by hand. Not given curve might not have an asymptote or possess symmetry.) But the guidelines provide all the information you need A. Domain It's often useful to start by determining the domain D of f, that is, the set B. Intercepts The y-intercept is f(o) and this tells us where the curve intersects the of values of x for which f(x) is defined y-axis. To find the x-intercepts, we set y-0and solve for xã(You can omit this step if the equation is difficult to solve.) ry (a) Even fusction: reflectional symmetry all x in D, that is, the equation of the curve is unchanged when x is replacea by -x, then f is an even function and the curve is symmetric about the y-axis. This means that our work is cut in half. If we know what the curve looks like for 0, then we need only reflect about the y-axis to obtain the com- plete curve [see Figure 3(a). Here are some examples: y-ey-ry x). and for all x in D, then f is an odd function and the curve is symmetric about the origin. Again we can obtain the complete curve if we know what it looks like for x0. [Rotate 180Â° about the origin; see Figure 3(b).] Some b) Oud function rotational symmetry FIGURE 3 simple examples of odd functions are y-xy-x'y - and y-sin

What are the answers for all of these questions? I am confused on how to solve for these.

1.

2.

3.

4.

Show transcribed image text