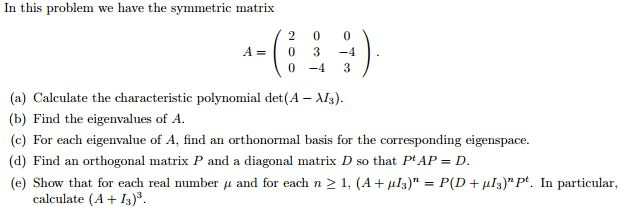MATA23H3 Lecture Notes - Lecture 22: Diagonal Matrix, Diagonalizable Matrix, Eigenvalues And Eigenvectors
Document Summary
Mata23 - lecture 22 - properties of eigenvalues, diagonalization, and multiplicity. Properties of eigenvalues: if a has eigenvalues 1, 2, . , n (repeated according to multiplicity), then deta = 1 2 . Det(a i) is a polynomial of degree n. , n are roots of det(a i) = 0. Det(a i) = ( 1 )( 2 ) . ( n ) Set = 0, deta = 1 2 . N: example 3: let a = [aij] be a 3 3 matrix and have its characteristic polynomial det(a i) = P( ) = det(a i) = 3 + 3 2. P(1) = 1 + 3 2 = 0. P( ) = 3 + + 2 2. = ( 2 + 1) + 2( 1) = ( + 1)( + 1) + 2( 1) = ( + 1)[ ( + 1) 2] = ( + 1)( 2 + 2) = ( + 1)( 1)( + 2), set = 0.