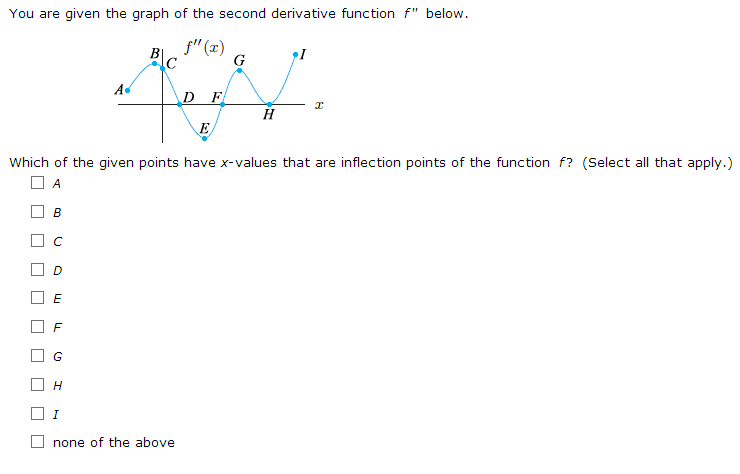
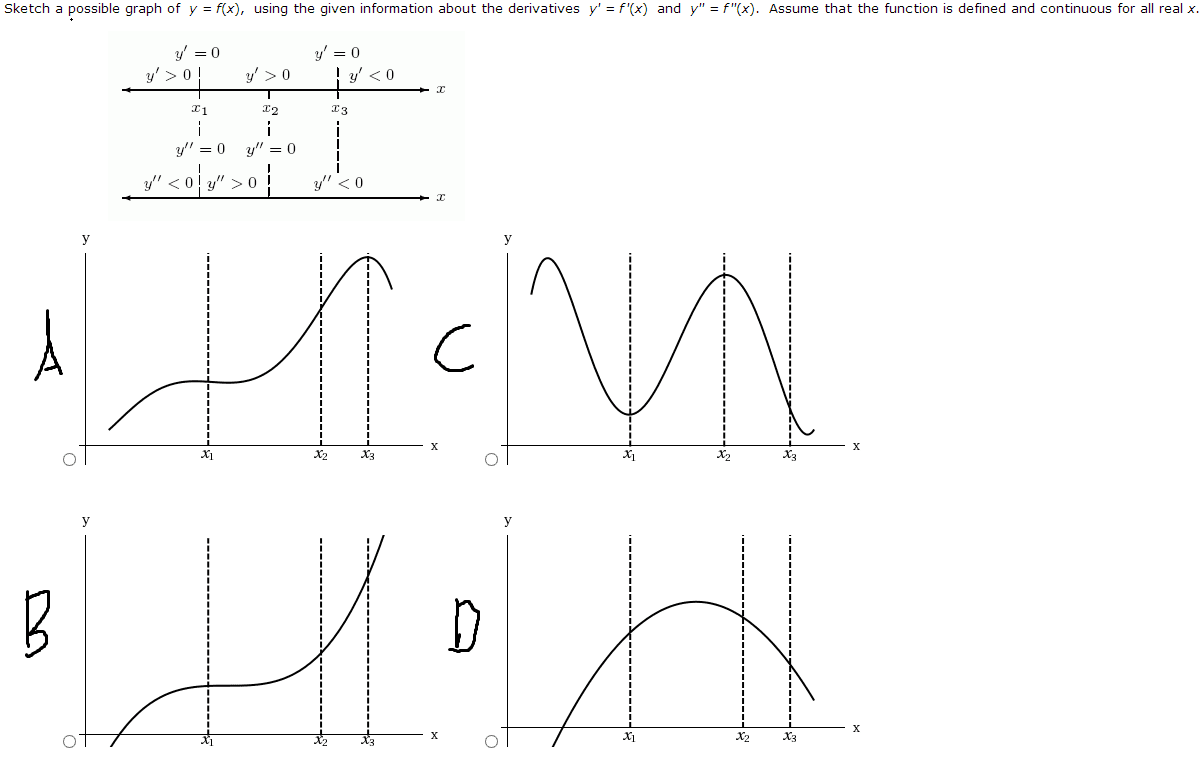MATH 105 Lecture Notes - Lecture 7: Maxima And Minima

42 views2 pages

Verified Note

goldgoat17

28 Jan 2019

School

Department

Course

Professor

For unlimited access to Class Notes, a Class+ subscription is required.

MATH 105 verified notes

7/40View all

MATH 105 Lecture 6: MATH 105 Lecture 6 Partial Derivatives and Maximum_minimum Problems Con’t

MATH 105 Lecture Notes - Lecture 7: Maxima And Minima

MATH 105 Lecture 8:

Document Summary

Math 105 lecture 7 partial derivatives and maximum/minimum problems con"t. Definitions of local extrema and theorem 12. 13 (12. 8, p 939) A function has a local maximum value at (a,b) if f(x,y) = f(a,b) for all (x,y) in the domain of f in some open disk centered at (a,b). A function f has a local minimum value at (a,b) if f(x,y) >/= f(a,b) for all (x,y) in the domain of f in some open disk centered at (a,b). Local maximum and local minimum values are also local extreme values or local extrema. If f has a local maximum or minimum value at (a,b) and the partial derivatives fx and fy exist at (a,b), then fx(a,b) = fy(a,b) = 0. Suppose f has a local maximum value at (a,b). the function of one variable g(x) = f(x,b), obtained by holding y=b fixed, also has a local maximum at (a,b). However, g"(a) = fx(a,b); therefore fx(a,b) = 0.

Related Questions

Q1)

---------------------------------------------------------------------------------

Q2)

---------------------------------------------------------------------------------

Q3)

---------------------------------------------------------------------------------

Q4)

---------------------------------------------------------------------------------

Q5)

---------------------------------------------------------------------------------

Q6)

---------------------------------------------------------------------------------

Q7)

If U and V are positive constants, find all critical points of the function. (Enter your answers as a comma-separated list.) F(t) = Ue t + Ve -t t = Find all critical points of f(x) = 20 x 2 e - 0.3x and classify them as local minima of ,maxima. x = (smaller value) This critical point is a . x = (larger value) This critical point is a . Consider f(x) = x 8 (7 - x) 9. Find f '(x) and simplify your answer. f '(x) = Find all critical points of f(x) and then use the first derivation test to determine local maxima and minima. f(x) has a at x = (smallest value) Local Maximum OR Minimum OR Neither f(x) has a at x = Local Maximum OR Minimum OR Neither f(x) has a at x = (largest value) Local Maximum OR Minimum OR Neither Find the inflection points of f(t) = t 4 + t 3 - 18t 2 +8. Give exact answer. t = (smallest value) t = (largest value) Sketch a possible of y = f(x), using the given information about derivation y' = f'(x) and y" = f"(x). Assume that the function is defined and continuous for all real x. Let f be a function f(x) > 0 for all x. Let g = 1/f. If f is increasing in an interval around x 0, what about g? g is increasing in an interval x 0. g is zero in an interval around x 0. g is decreasing in an interval around x 0. We cannot tell whether g is increasing or decreasing in an interval around x 0. g is constant in an interval around x 0. If f has a local maximum at x 1, what about g? g has a local maximum at x 1. g has both a local minimum and a local maximum at x 1. We cannot tell whether g has a local minimum or a local maximum at x 1. g has an inflection point at x 1. g has a local minimum at x 1. If f is a concave down at x 2, what about g? g is increasing at x 2. g is flat at x 2. We cannot tell whether g is concave up of concave down at x 2. g is concave down at x 2. g is concave up at x 2. You are given the graph of the second derivation function f" below. Which of the given have x-values that are inflection points of the function f? (Select all the apply.) A B C D E F G H I none of the above

The three cases in the First Derivative Test cover the situations one commonly encounters but do not exhaust all possibilities. Consider the functions f, g, and h whose values at 0 are all 0 and, for x ≠ 0.

(a) Show that 0 is a critical number of all three functions but their derivatives change sign infinitely often on both sides of 0.

(b) Show that f has neither a local maximum nor a local minimum at 0, t has a local minimum, and h has a local maximum.

azureshark0

MATH 105 Lecture Notes - Lecture 7: Maxima And Minima

MATH 105 Lecture 6: MATH 105 Lecture 6 Partial Derivatives and Maximum_minimum Problems Con’t

MATH 105 Lecture Notes - Lecture 7: Maxima And Minima

MATH 105 Lecture 8:

Document Summary

Get access

Related textbook solutions

Calculus

Single Variable Calculus: Early Transcendentals

CALCULUS:EARLY TRANSCENDENTALS

Related Documents

MATH 105 Lecture 6: MATH 105 Lecture 6 Partial Derivatives and Maximum_minimum Problems Con’t

MATH 105 Midterm: MATH105 Exam 3

MATH 105 Midterm: MATH105 Exam 3 Solutions

Related Questions