MATH 103 Lecture 3: Geometric Series
MATH 103 verified notes
3/17View all
Document Summary
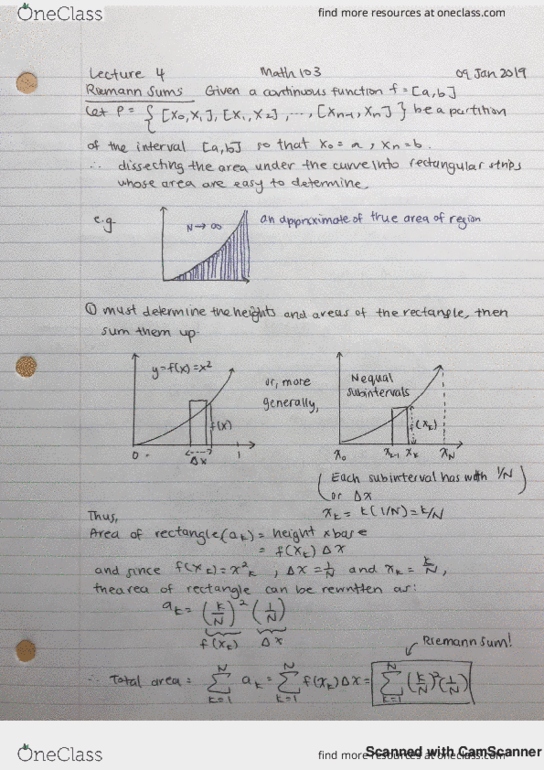
K3 t 3k 2 t 3kt ( kt 173 - k 3. I calculate this is of the form want. Know lakh al ) such sums are called. Cancel out t t telescopihgsurfrsn (2/3-13) (3/3-2/3) (143-3/3)t. E formula prove to similarly , we can use. [ ie k ] sum of: g . ( telescoping sums for differences of consecutive terms. = z t it t t t ninh , we know k +1 ft. Keith : eik - it ) - if t. Let r be a real number then the sum it r tr w. In general we can have at art ar tar. For a series aotaitaztaz t t an to be a geometric series we must have dat. mn consider we have infinitely many numbers aot out. Azt we can the sum info ai the nth partial sum. Then we define oak linty if, ay exist converges does not exist diverges: g .