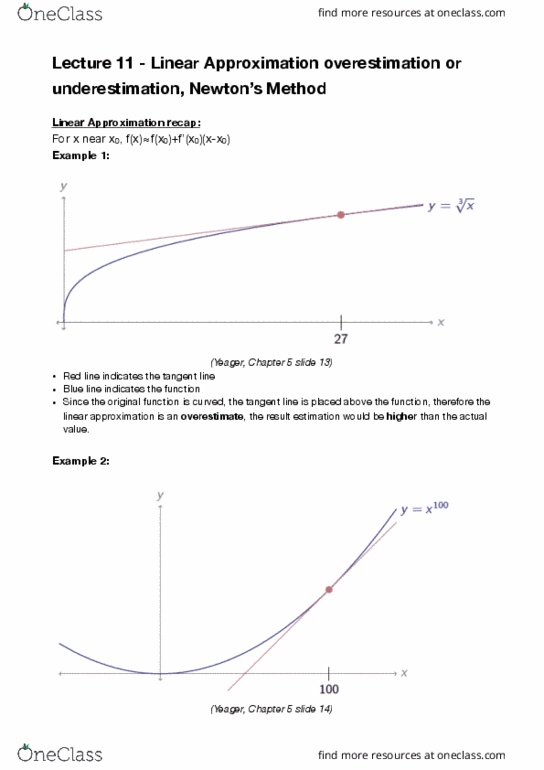
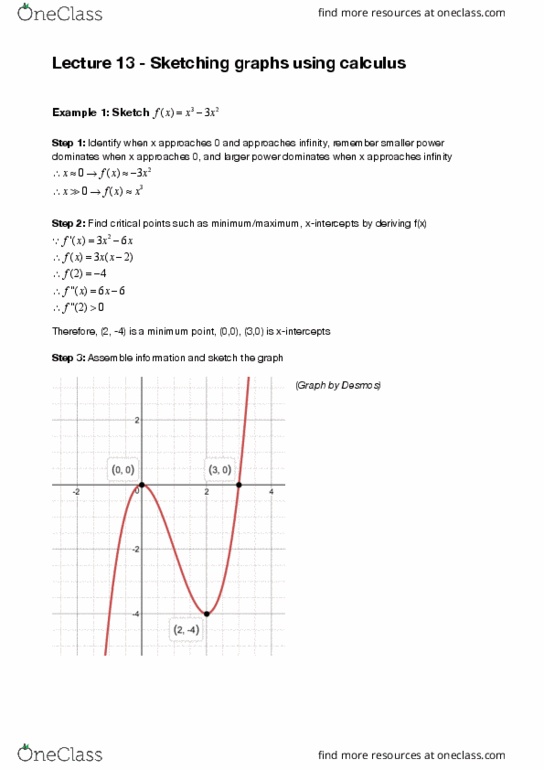
MATH 102 Lecture Notes - Lecture 12: Aphid, Asymptote, Ant Colony
MATH 102 verified notes
12/37View all
Document Summary
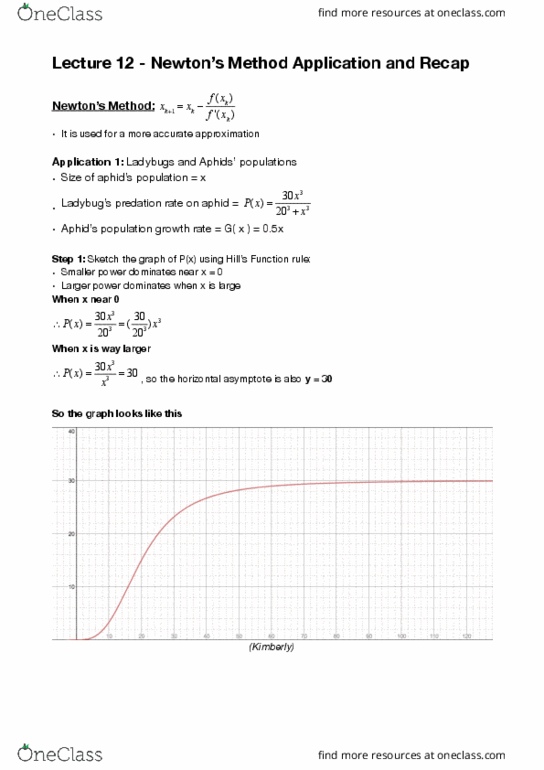
= xk f (xk ) f "(xk : it is used for a more accurate approximation. Application 1: ladybugs and aphids" populations: size of aphid"s population = x, ladybug"s predation rate on aphid = # 203 + x3: aphid"s population growth rate = g( x ) = 0. 5x. Step 1: sketch the graph of p(x) using hill"s function rule: smaller power dominates near x = 0, larger power dominates when x is large. , so the horizontal asymptote is also y = 30. By graphing g(x) & p(x), the graph becomes like this: Green line - > g(x) red line -> p(x) (kimberly) Key points: stable equilibrium: intersection points > g(x) = p(x, unstable equilibrium: the intervals between the intersection points > g(x) > p(x) or p(x) > Step 3: find out the rst intersection point using newton"s method { 0 < x < 20 } 2 + 203 = 0 x using newton"s method: # xk +1.