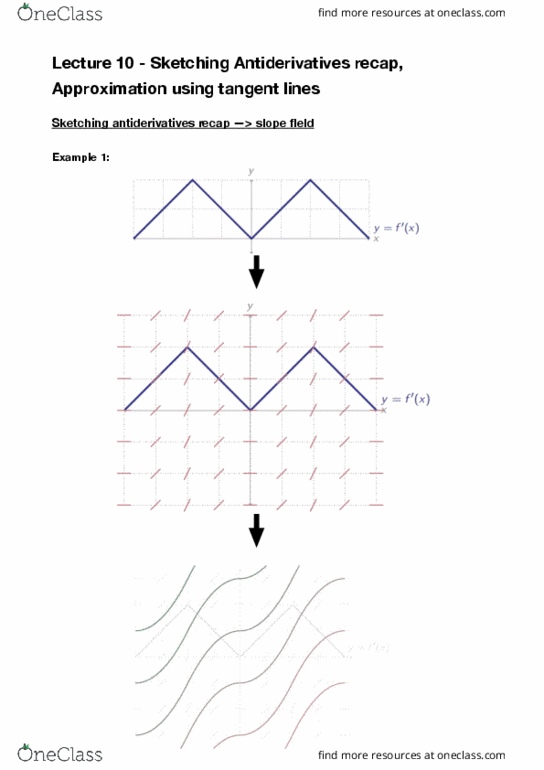
MATH 102 Lecture 10: Sketching Antiderivatives recap, Approximation using tangent lines
MATH 102 verified notes
10/37View all
Document Summary
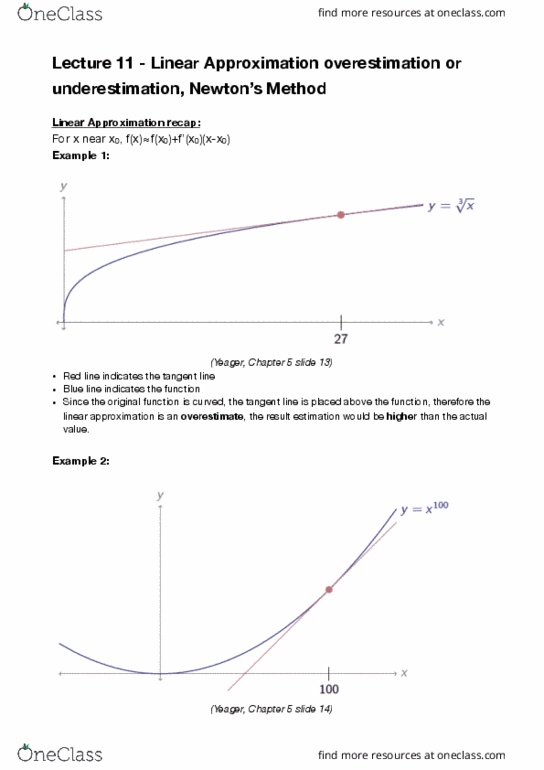
Use of tangent lines: to approximate a function using a xed point > assume that the tangent line on the. Step 1: choose a nice value that you know, such as 9, because # , which results in # y " = Step 3: as we know (9,3) is on the function, nd the tangent line when x = 9 f "(9) = , so we know slope = 1/6, so the function becomes # y = We now put (9,3) back into this tangent line function, which results in# y = Step 4: put when x = 10 into # y = Step 5: check if the approximation is correct ( 10 )2 = 10. Therefore, the approximation is pretty close to the actual value of ! 0 ( y y0 ) = m(x x0 ) F (x0 ) = f "(x0 )(x x0 ) (x x0 ) = f (x0 ) f "(x0 )