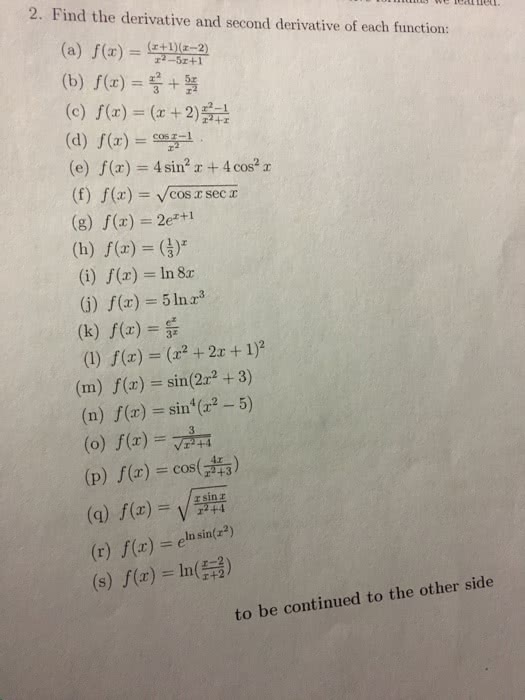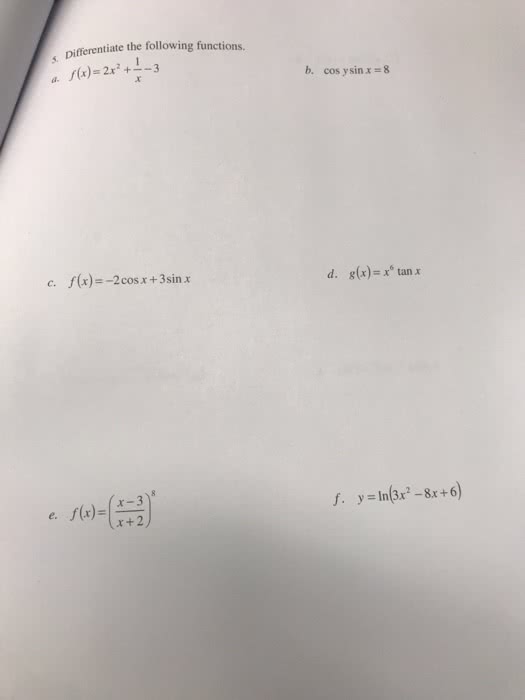MATH116 Lecture 15: ContinuityExamples
9 Dec 2015
School
Department
Course
Professor
Document Summary
If g(x) is continuous at x = a and f (y) is continuous at g(a), then (f g)(x) = f (g(x)) is continuous at x = a. Where are the following functions continuous: h(x) = sin(x2, f (x) = ln(1 + cos(x)) Solution: we have h(x) = f (g(x)) where (1) Now g is continuous on r since it is a polynomial, and f is also continuous everywhere. Therefore by theorem 1, f (x) = f (g(x)) is continuous wherever it is de ned. Now ln(1 + cos(x)) is de ned when 1 + cos(x) > 0. Note that the range of 1 + cos(x) is [0, 1] since 1 cos(x) 1 so ln(1+cos(x)) is unde ned when 1+cos(x) = 0 cos(x) = 1 and this happens when x = , 3 , . Thus f has discontinuities when x is an odd multiple of and is continuous on the intervals between these values.
