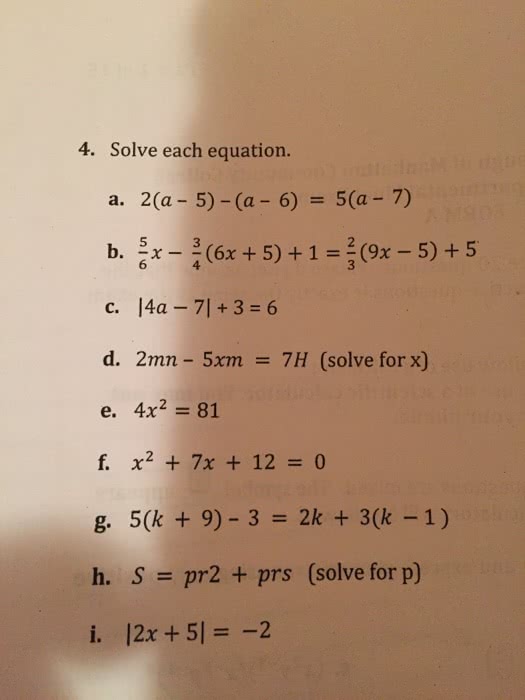MATH116 Lecture Notes - Lecture 8: Inverse Function

19 views3 pages

cyanimpala400

9 Dec 2015

School

University of Waterloo

Department

Mathematics

Course

MATH116

Professor

Fiona Dunbar

For unlimited access to Class Notes, a Class+ subscription is required.

Document Summary

Practice solutions 1: let f (x) = 2x 1 and g(x) = x + 3. Find the following: (a) f (g(1)) (e) f (f ( 2)) (b) g(f (7)) (c) f (g(x)) (d) g(f (x)) (f) g(g(6)) (g) f (f (x)) (h) g(g(x)) 1 + 3) 1 = 4 1 = 3. (a) f (g(1)) = 2(g(1)) 1 = 2( 14 1 + 3 = 4. (c) f (g(x)) = 2(g(x)) 1 = 2 x + 3 1. 2x 1 + 3 = (e) f (f ( 2)) = 2(f ( 2)) 1 = 2(2( 2) 1) 1 = 2( 5) 1 = 11. This could be simpli ed as (cid:113) 3 2x x 1 , but. 1 x 2 1 f (x) 1 = x 2 1 to be nonzero. x 2 (cid:54)= 1, or x 2 (cid:54)= 1, which implies x (cid:54)= 3. Since the numerator is positive, the sign of the left hand side.

Related Questions

Problem 4 Circle your answer. a) (6 points) If f(x) = 2x + 3x2 - 361 + 5, then the tangent line to the graph y= f(x) is horizontal when i) 1 = -2,3 ii) I = 2,-3 iii) r = 0 iv) not listed b) [6 points] Suppose Given h(x) = f(g(T)), where g(2) = 3, g'(2) = 7, f'(2) = -1 and 1'(3) = -2. Then h'(2) is equal to i) - 1 ii) -2 iii) - 14 iv) not listed (x+3)(1 - 1)3 c) (6 points) The function f(1) == (x2 - 2x + 1)(x + 3) wa has vertical asymptotes at i) x = -3,0 ii) = -3,0,1 iii) x = 0,1 iv) not listed d) (6 points] The solution to the initial value problem v'(x) = 473 – cos(x) +e", y(0) = 3 is i) y(x) = x + sin(x) + e* + 2 ii) y(I) = x4 – sin(x) +et+2 iii) y(x) = 2* – sin(1) + et + 3 iv) not listed

Please I need quick help these questions they are due so soon. Thanks