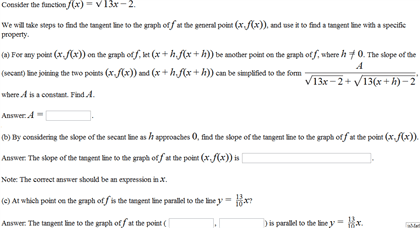MATH 154 Lecture Notes - Lecture 8: Constant Function
211 views2 pages
Verified Note
22 Sep 2018
School
Department
Course
Professor
MATH 154 verified notes
8/38View all
Document Summary
To find the slope of a tangent line, take the derivative as the slope. Recall; the derivative of a function is defined as (cid:4666)(cid:4667)=lim 0(cid:4666)(cid:3051)+ (cid:4667) (cid:4666)(cid:3051)(cid:4667) The expression in the limit gives the slope of the secant line from points x" to. The derivative (eg f"(x)) gives the slope of the tangent line passing through the point x". The normal line is perpendicular to the tangent line, & also passes through the same point the tangent line passes through. The slope of the tangent line is denoted as mt, the slope of the normal line is mn. Mt mn = -1 (because they"re perpendicular) Eg if mt is 6, mn is -1/6. If we"re looking at a constant function (f(x) = c), the derivative is always 0. The derivative of a constant is 0, so the derivative of a constant function is 0. The derivative of a function f(x) = cx (with c as a constant) = c.
Get access
Grade+
$40 USD/m
Billed monthly

Homework Help
Study Guides
Textbook Solutions
Class Notes
Textbook Notes
Booster Class
10 Verified Answers
Class+
$30 USD/m
Billed monthly

Homework Help
Study Guides
Textbook Solutions
Class Notes
Textbook Notes
Booster Class
7 Verified Answers