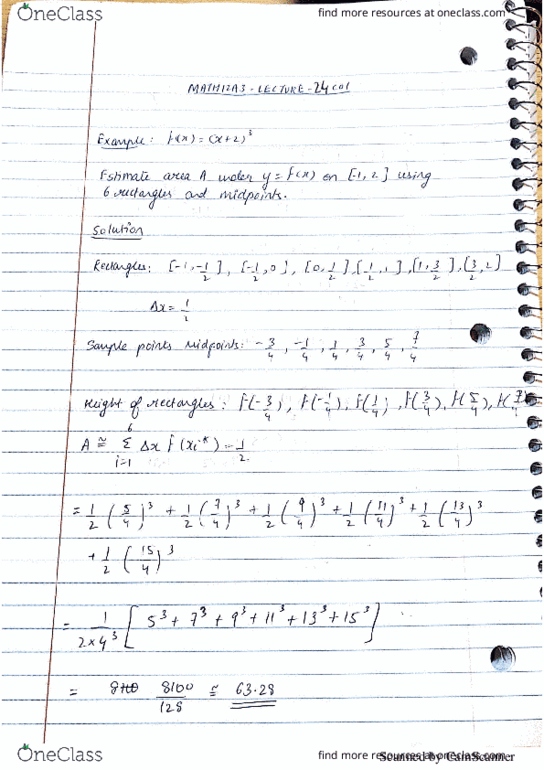MATH 1ZA3 Lecture 23: Lecture 23
MATH 1ZA3 verified notes
23/25View all
Document Summary
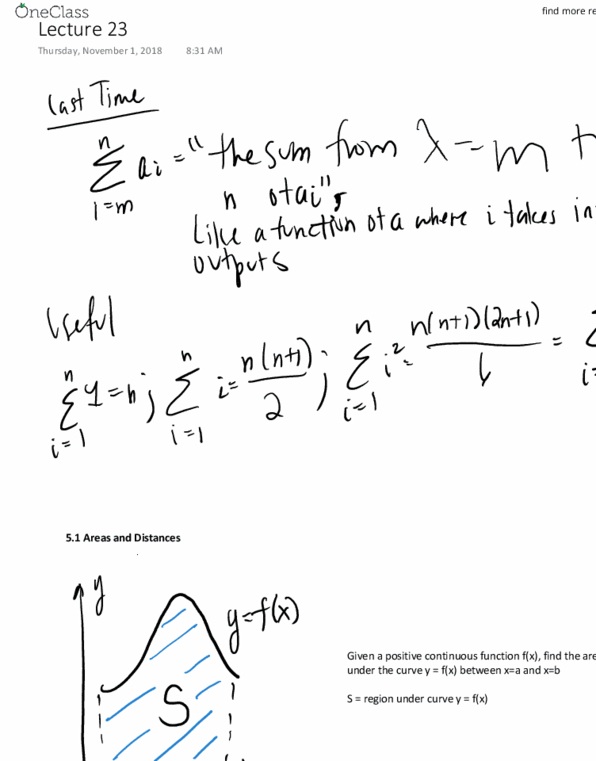
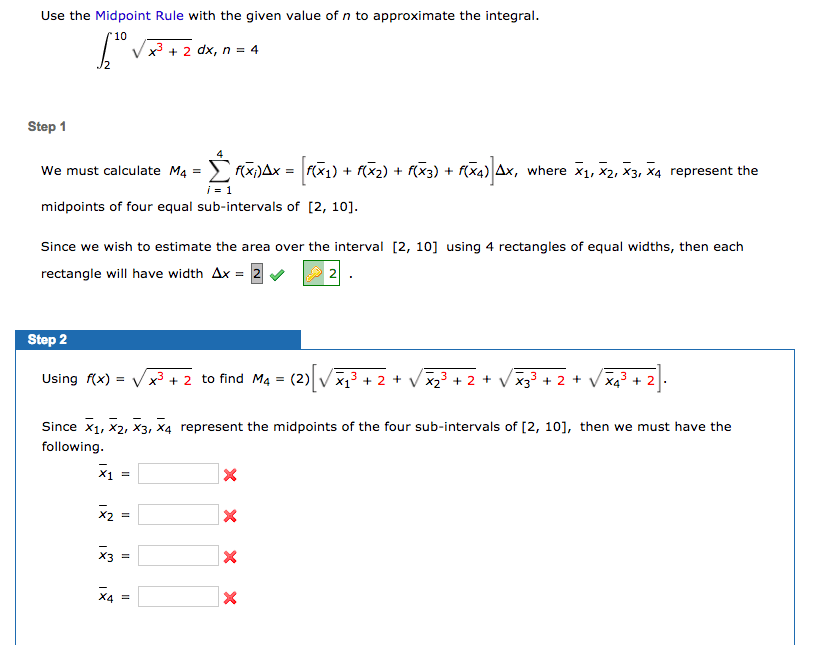
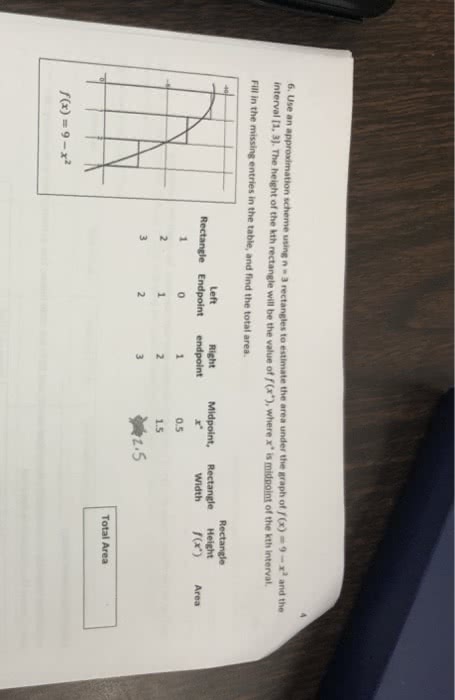
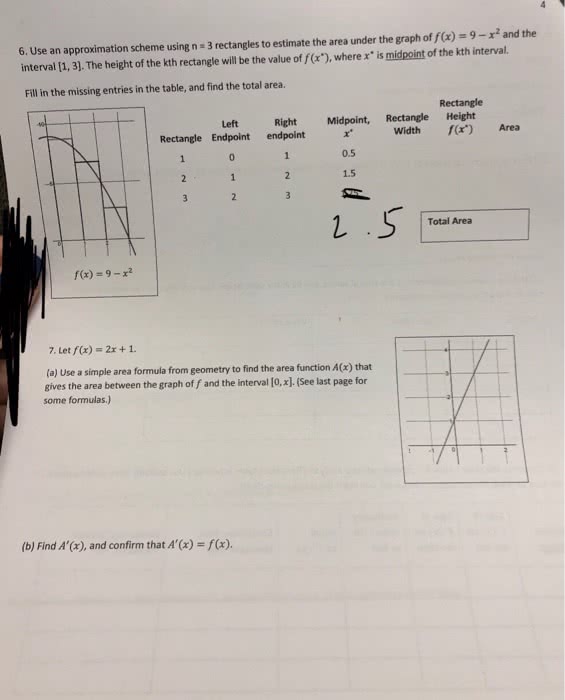
Given a positive continuous function f(x), find the area under the curve y = f(x) between x=a and x=b. S = region under curve y = f(x) Goal find a = area of s. Big idea cut up s into thin vertical slices and approximate each slice by a rectangle. Divide up [a,b] into n mini-intervals each of which has same width. Approximate si (it"s slice) = slice under y = f(x) between x = x i-1 and x = xi with reactant of width x and heights f(xi) As we increase n (i. e. the # of slices) we get a better and better approximation to a. We define the area a under y=f(x) from x=a to x=b to be lim. [note it can be shown that this limit exists since f(x) is continuous] No good reason to approximate si with a rectangle whose heigh was f(xi) and not f(x) for some other x as an element of [xi-1, xi]